题目内容
3.如图是某几何体的三视图(单位:cm),则该几何体的表面积是14+2$\sqrt{13}$cm2,体积为4cm3.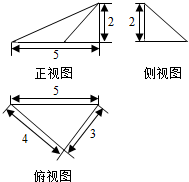
分析 判断得出该几何体是三棱锥,利用题中数据,即可求解几何体的表面积、体积.
解答 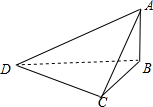 解:根据三视图得出:该几何体是三棱锥,AB=2,BC=3,DB=5,CD=4,
解:根据三视图得出:该几何体是三棱锥,AB=2,BC=3,DB=5,CD=4,
AB⊥面BCD,BC⊥CD,
∴几何体的表面积是$\frac{1}{2}×3×4$+$\frac{1}{2}×3×2$+$\frac{1}{2}×5×2$+$\frac{1}{2}×4×\sqrt{13}$=14+2$\sqrt{13}$
其体积:$\frac{1}{3}$×S△CBD×AB=$\frac{1}{3}×\frac{1}{2}×3×4×2$=4,
故答案为:14+2$\sqrt{13}$;4.
点评 本题考查了三棱锥的三视图的运用,仔细阅读数据判断恢复直观图,关键是确定几何体的形状,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
13.已知f(x)=sin(2015x+$\frac{3π}{8}$)+sin(2015x-$\frac{π}{8}$)的最大值为A,若存在实数x1,x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )
| A. | $\frac{\sqrt{2}π}{2015}$ | B. | $\frac{2\sqrt{2}π}{2015}$ | C. | $\frac{2π}{2015}$ | D. | $\frac{4π}{2015}$ |
14.如果函数y=|cos(ωx+$\frac{π}{4}$)|的图象关于直线x=π对称,则正实数ω的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为 4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
18.在一次数学测试(满分为150分)中,某校2000名考生的分数X近似服从正态分布N(100,σ2).据统计,分数在100~110分段的考生共440人,估计分数在90分以上的考生大概有( )人.
| A. | 560 | B. | 880 | C. | 1120 | D. | 1440 |
8.已知向量|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则|2$\overrightarrow{b}$-$\overrightarrow{a}$|=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
13.等比数列{an}中,a2=$\frac{1}{4}$,a6=4,记{an}的前n项积为Tn,则T7=( )
| A. | 1 | B. | 1或一1 | C. | 2 | D. | 2或一2 |