题目内容
【题目】如果l是空间中的一条直线，
是空间中的一个平面，判断下列命题的真假.
（1）l与要么相交，要么不相交；
（2）要么l在内，要么l在外；
（3）要么l与平行，要么l在内.
【答案】（1）真命题；（2）真命题；（3）假命题.
【解析】
根据空间直线与平面的位置关系有直线在平面内和直线在平面外，而直线在平面外又分为直线与平面相交和直线与平面平行,可判断这三个命题的真假.
由空间直线与平面的位置关系有直线在平面内和直线在平面外，而直线在平面外又分为直线与平面相交和直线与平面平行.
(1) l与
要么相交，要么不相交,(1)是真命题.
(2) 要么l在内，要么l在外，(2)是真命题.
(3) 要么l与平行，要么l在内，要么l与相交,所以（3）是假命题.
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
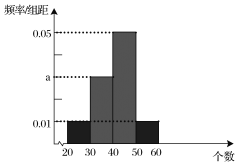
暑假作业北京艺术与科学电子出版社系列答案【题目】某工厂生产某种型号的电视机零配件，为了预测今年
月份该型号电视机零配件的市场需求量，以合理安排生产，工厂对本年度
月份至
月份该型号电视机零配件的销售量及销售单价进行了调查，销售单价
（单位：元）和销售量
（单位：千件）之间的组数据如下表所示：
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
（1）根据1至月份的数据，求关于的线性回归方程（系数精确到
）；
（2）结合（1）中的线性回归方程，假设该型号电视机零配件的生产成本为每件
元，那么工厂如何制定月份的销售单价，才能使该月利润达到最大（计算结果精确到
）？
参考公式：回归直线方程
，其中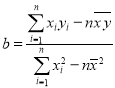
.
参考数据：
.
【题目】某高中尝试进行课堂改革.现高一有
两个成绩相当的班级，其中
班级参与改革，
班级没有参与改革.经过一段时间，对学生学习效果进行检测，规定成绩提高超过
分的为进步明显，得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
（1）是否有
的把握认为成绩进步是否明显与课堂是否改革有关?
（2）按照分层抽样的方式从
班中进步明显的学生中抽取
人做进一步调查，然后从人中抽
人进行座谈，求这人来自不同班级的概率.
附：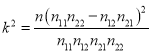
，当
时，有的把握说事件与有关.
