题目内容
已知正方形ABCD的边长为2,P、Q分别为边AB、DA上的点.设∠BCP=α,∠DCQ=β,若△APQ的周长为4,则α+β=( )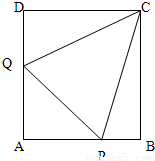
A.15°
B.30°
C.45°
D.60°
【答案】分析:延长AB到E,使|BE|=|DQ|,连接CE,利用SAS得到△CDQ≌△CBE,进而利用锐角三角函数定义表示出tanα+tanβ与tanαtanβ,利用两角和与差的正切函数公式化简tan(α+β),将表示出tanα+tanβ与tanαtanβ代入计算求出tan(α+β)的值,即可求出α+β的度数.
解答: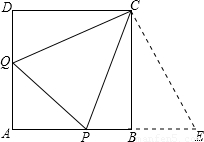 解:延长AB到E,使|BE|=|DQ|,连接CE,
解:延长AB到E,使|BE|=|DQ|,连接CE,
∵四边形ABCD为正方形,
∴∠D=∠CBE=90°,|CD|=|CB|,
∴△CDQ≌△CBE(SAS),
∴∠BCE=∠DCQ=β,
在Rt△CDQ中,设|DQ|=|BE|=x,|CD|=2,
可得x=2tanβ,AQ=2-2tanβ,
在Rt△CPB中,设|PB|=y,|CB|=2,
可得y=2tanα,|AP|=2-2tanα,
又△APQ的周长为4,
∴|PQ|=4-(|AQ|+|AP|)=4-(2-2tanβ+2-2tanα)=2(tanα+tanβ),即tanα+tanβ= |PQ|,
|PQ|,
在Rt△APQ中,根据勾股定理得:|PQ|=(2-2tanβ)2+(2-2tanα)2,
整理得:tanαtanβ=1- |PQ|,
|PQ|,
∴tan(α+β)=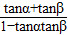 =
=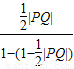 =1,
=1,
则α+β=45°.
故选C
点评:此题考查了两角和与差的正切函数公式,锐角三角函数定义,全等三角形的判定与性质,勾股定理,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.
解答:
 解:延长AB到E,使|BE|=|DQ|,连接CE,
解:延长AB到E,使|BE|=|DQ|,连接CE,∵四边形ABCD为正方形,
∴∠D=∠CBE=90°,|CD|=|CB|,
∴△CDQ≌△CBE(SAS),
∴∠BCE=∠DCQ=β,
在Rt△CDQ中,设|DQ|=|BE|=x,|CD|=2,
可得x=2tanβ,AQ=2-2tanβ,
在Rt△CPB中,设|PB|=y,|CB|=2,
可得y=2tanα,|AP|=2-2tanα,
又△APQ的周长为4,
∴|PQ|=4-(|AQ|+|AP|)=4-(2-2tanβ+2-2tanα)=2(tanα+tanβ),即tanα+tanβ=
 |PQ|,
|PQ|,在Rt△APQ中,根据勾股定理得:|PQ|=(2-2tanβ)2+(2-2tanα)2,
整理得:tanαtanβ=1-
 |PQ|,
|PQ|,∴tan(α+β)=
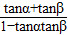 =
=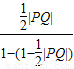 =1,
=1,则α+β=45°.
故选C
点评:此题考查了两角和与差的正切函数公式,锐角三角函数定义,全等三角形的判定与性质,勾股定理,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知正方形ABCD的边长为1,设
=
,
=
,
=
,则|
-
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|
 已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1,
已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1, 如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.
如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.