Question

【题目】已知曲线的方程为，则下列结论正确的是（ ）

A.当时，曲线为椭圆，其焦距为

B.当时，曲线为双曲线，其离心率为

C.存在实数使得曲线为焦点在轴上的双曲线

D.当时，曲线为双曲线，其渐近线与圆相切

Answer 1

【答案】B

【解析】

根据的取值和椭圆、双曲线的几何性质可确定的正误；根据方程表示双曲线可构造不等式，确定的正误；根据直线与圆位置关系的判定可知的正误.

对于，当时，曲线的方程为，轨迹为椭圆，

焦距，错误；

对于，当时，曲线的方程为，轨迹为双曲线，

则，，离心率，正确；

对于，若曲线表示焦点在轴上的双曲线，则，解集为空集，

不存在实数使得曲线为焦点在轴上的双曲线，错误；

对于，当时，曲线的方程为，其渐近线方程为，

则圆的圆心到渐近线的距离，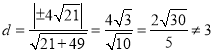

双曲线渐近线与圆不相切，错误.

故选：.