题目内容
【题目】为了增强学生的冬奥会知识，弘扬奥林匹克精神，北京市多所中小学校开展了模拟冬奥会各项比赛的活动.为了了解学生在越野滑轮和旱地冰壶两项中的参与情况，在北京市中小学学校中随机抽取了10所学校，10所学校的参与人数如下：
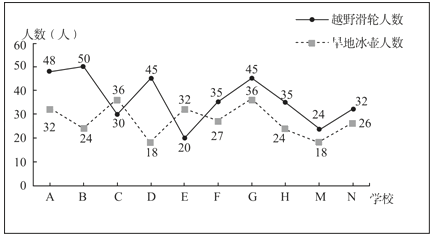
（Ⅰ）现从这10所学校中随机选取2所学校进行调查.求选出的2所学校参与越野滑轮人数都超过40人的概率；
（Ⅱ）现有一名旱地冰壶教练在这10所学校中随机选取2所学校进行指导，记X为教练选中参加旱地冰壶人数在30人以上的学校个数，求X的分布列和数学期望；
（Ⅲ）某校聘请了一名越野滑轮教练，对高山滑降、转弯、八字登坡滑行这3个动作进行技术指导.规定：这3个动作中至少有2个动作达到“优”，总考核记为“优”.在指导前，该校甲同学3个动作中每个动作达到“优”的概率为0.1.在指导后的考核中，甲同学总考核成绩为“优”.能否认为甲同学在指导后总考核达到“优”的概率发生了变化？请说明理由.
【答案】（Ⅰ）
（Ⅱ）见解析，
（Ⅲ）见解析
【解析】
（Ⅰ）记“选出的两所学校参与越野滑轮人数都超过40人”为事件S，从这10所学校中随机选取2所学校进行调查，可得基本事件总数为
.参与越野滑轮人数超过40人的学校共4所，随机选择2所学校共
种，利用古典概率计算公式即可得出概率.
（Ⅱ）X的所有可能取值为0，1，2，参加旱地冰壶人数在30人以上的学校共4所.利用超几何分布列计算公式即可得出.
（Ⅲ）答案不唯一.示例：虽然概率非常小，但是也可能发生，一旦发生，就有理由认为指导后总考核达到“优”的概率发生了变化.
（Ⅰ）记“选出的两所学校参与越野滑轮人数都超过40人”为事件S，现从这10所学校中随机选取2所学校进行调查，可得基本事件总数为.
参与越野滑轮人数超过40人的学校共4所，随机选择2所学校共
种，
所以
（Ⅱ）X的所有可能取值为0，1，2，参加旱地冰壶人数在30人以上的学校共4所.
，
，
.
X的分布列为：
X | 0 | 1 | 2 |
P |
|
|
|
.
（Ⅲ）答案不唯一.
答案示例1：可以认为甲同学在指导后总考核为“优”的概率发生了变化.理由如下：
指导前，甲同学总考核为“优”的概率为：
.
指导前，甲同学总考核为“优”的概率非常小，一旦发生，就有理由认为指导后总考核达到“优”的概率发生了变化.
答案示例2：无法确定.理由如下：
指导前，甲同学总考核为“优”的概率为：.
虽然概率非常小，但是也可能发生，所以，无法确定总考核达到“优”的概率发生了变化.
