题目内容
(本小题满分14分)
设数列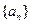 的通项公式为
的通项公式为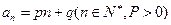 . 数列
. 数列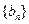 定义如下:对于正整数m,
定义如下:对于正整数m,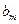 是使得不等式
是使得不等式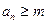 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若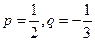 ,求
,求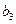 ;
;
(Ⅱ)若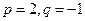 ,求数列
,求数列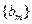 的前2m项和公式;
的前2m项和公式;
(Ⅲ)是否存在p和q,使得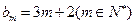 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
设数列
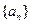 的通项公式为
的通项公式为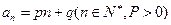 . 数列
. 数列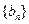 定义如下:对于正整数m,
定义如下:对于正整数m,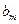 是使得不等式
是使得不等式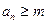 成立的所有n中的最小值.
成立的所有n中的最小值.(Ⅰ)若
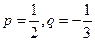 ,求
,求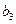 ;
;(Ⅱ)若
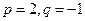 ,求数列
,求数列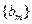 的前2m项和公式;
的前2m项和公式;(Ⅲ)是否存在p和q,使得
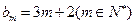 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.(Ⅰ)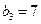
(Ⅱ)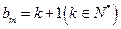
(Ⅲ)存在p和q,使得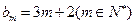 ;p和q的取值范围分别是
;p和q的取值范围分别是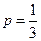 ,
,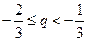 .
.
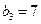
(Ⅱ)
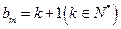
(Ⅲ)存在p和q,使得
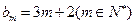 ;p和q的取值范围分别是
;p和q的取值范围分别是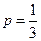 ,
,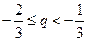 .
. (Ⅰ)由题意,得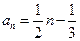 ,解
,解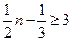 ,得
,得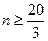 . ---------------2分
. ---------------2分
∴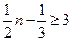 成立的所有n中的最小整数为7,即
成立的所有n中的最小整数为7,即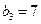 .-----------4分
.-----------4分
(Ⅱ)由题意,得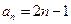 ,对于正整数,由
,对于正整数,由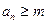 ,得
,得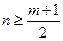 . -------------------6分
. -------------------6分
根据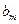 的定义可知:当
的定义可知:当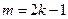 时,
时,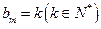 ;当
;当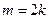 时,
时,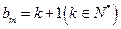 .
.
∴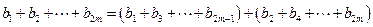
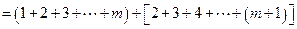
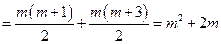 . ---------------------9分
. ---------------------9分
(Ⅲ)假设存在p和q满足条件,由不等式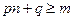 及
及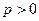 得
得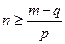 .------10分
.------10分
∵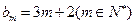 ,根据
,根据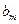 的定义可知,对于任意的正整数m都有
的定义可知,对于任意的正整数m都有
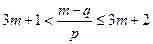 ,即
,即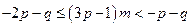 对任意的正整数m都成立.
对任意的正整数m都成立.
当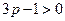 (或
(或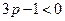 )时,得
)时,得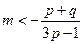 (或
(或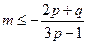 ),----12分
),----12分
这与上述结论矛盾!
当 ,即
,即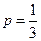 时,得
时,得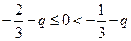 ,解得
,解得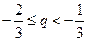 .
.
∴ 存在p和q,使得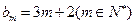 ;
;
p和q的取值范围分别是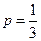 ,
,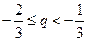 . ----------14分
. ----------14分
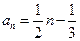 ,解
,解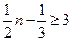 ,得
,得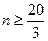 . ---------------2分
. ---------------2分∴
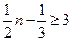 成立的所有n中的最小整数为7,即
成立的所有n中的最小整数为7,即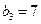 .-----------4分
.-----------4分(Ⅱ)由题意,得
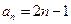 ,对于正整数,由
,对于正整数,由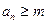 ,得
,得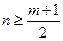 . -------------------6分
. -------------------6分根据
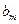 的定义可知:当
的定义可知:当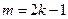 时,
时,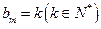 ;当
;当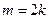 时,
时,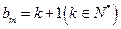 .
.∴
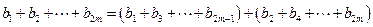
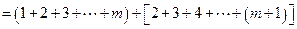
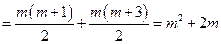 . ---------------------9分
. ---------------------9分(Ⅲ)假设存在p和q满足条件,由不等式
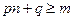 及
及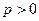 得
得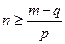 .------10分
.------10分∵
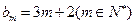 ,根据
,根据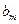 的定义可知,对于任意的正整数m都有
的定义可知,对于任意的正整数m都有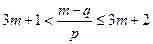 ,即
,即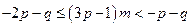 对任意的正整数m都成立.
对任意的正整数m都成立.当
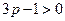 (或
(或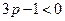 )时,得
)时,得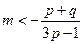 (或
(或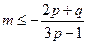 ),----12分
),----12分这与上述结论矛盾!
当
 ,即
,即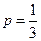 时,得
时,得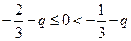 ,解得
,解得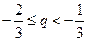 .
.∴ 存在p和q,使得
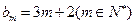 ;
;p和q的取值范围分别是
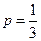 ,
,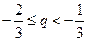 . ----------14分
. ----------14分
练习册系列答案
相关题目
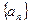 中,已知
中,已知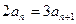 ,且
,且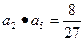 ,(1)求证:数列
,(1)求证:数列 是否为该数列的项?若是,是第几项?若不是,请说明理由。
是否为该数列的项?若是,是第几项?若不是,请说明理由。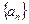 的首项
的首项 。
。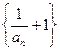 是等比数列,并求
是等比数列,并求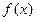 是偶函数,且对任意
是偶函数,且对任意 均有
均有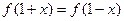 ,当
,当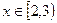 时,
时,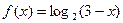 ,求使
,求使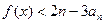 恒成立的
恒成立的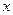 的取值范围。
的取值范围。 逐月递增且控制在2万件内;
逐月递增且控制在2万件内; 对任意的p、q
对任意的p、q 有ap+aq=ap+q,若a1=
有ap+aq=ap+q,若a1=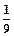 ,则a36="__________."
,则a36="__________." 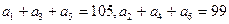 ,则
,则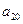 等于_ ____
等于_ ____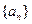 为等差数列,其前n项和为
为等差数列,其前n项和为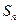 ,已知
,已知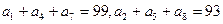 ,若对任意
,若对任意 都有
都有 成立,则k的值为( )
成立,则k的值为( )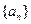 、
、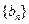 的前
的前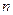 项和的比
项和的比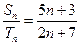 ,则
,则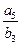 的值是
的值是 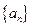 的前
的前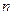 项的和为
项的和为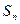 ,且
,且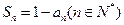 ,则
,则