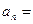题目内容
(本题14分)数列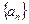 的首项
的首项 。
。
(1)求证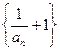 是等比数列,并求
是等比数列,并求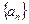 的通项公式;
的通项公式;
(2)已知函数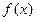 是偶函数,且对任意
是偶函数,且对任意 均有
均有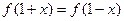 ,当
,当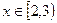 时,
时,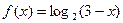 ,求使
,求使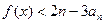 恒成立的
恒成立的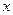 的取值范围。
的取值范围。
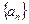 的首项
的首项 。
。(1)求证
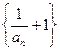 是等比数列,并求
是等比数列,并求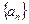 的通项公式;
的通项公式;(2)已知函数
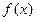 是偶函数,且对任意
是偶函数,且对任意 均有
均有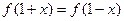 ,当
,当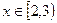 时,
时,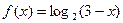 ,求使
,求使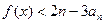 恒成立的
恒成立的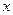 的取值范围。
的取值范围。(1)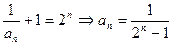 (2)
(2)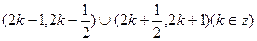
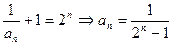 (2)
(2)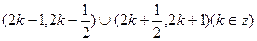
解:(1)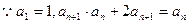
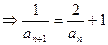
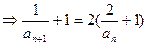
而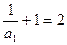
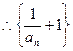 是首项为2公比为2的等比数列
是首项为2公比为2的等比数列
即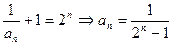 ……………………………………………4分
……………………………………………4分
(2)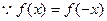
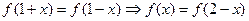
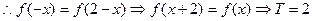
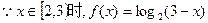
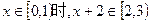
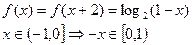
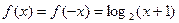
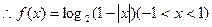 ……………………………………………8分
……………………………………………8分
令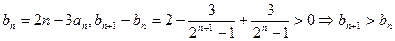
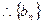 是递增数列,
是递增数列,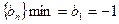
当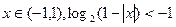
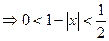
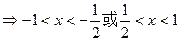 ……………………………………………12分
……………………………………………12分
又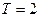
故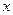 的取值范围是
的取值范围是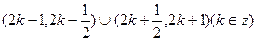 ………………14分
………………14分
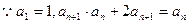
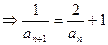
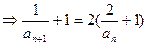
而
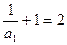
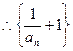 是首项为2公比为2的等比数列
是首项为2公比为2的等比数列即
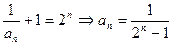 ……………………………………………4分
……………………………………………4分(2)
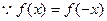
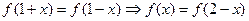
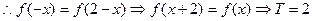
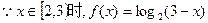
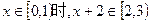
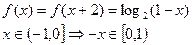
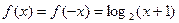
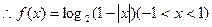 ……………………………………………8分
……………………………………………8分令
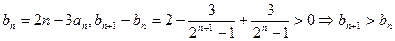
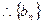 是递增数列,
是递增数列,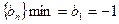
当
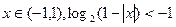
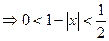
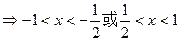 ……………………………………………12分
……………………………………………12分又
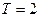
故
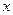 的取值范围是
的取值范围是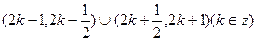 ………………14分
………………14分
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
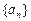 满足:
满足: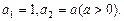 数列
数列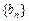 满足
满足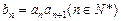 .
.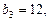 求
求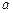 的值及
的值及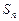 .
.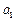 ,
,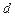 为实数,首项为
为实数,首项为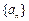 的前n项和为
的前n项和为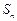 ,满
,满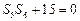 .(1)若
.(1)若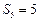 ,求
,求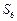 及
及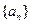 的通项公式为
的通项公式为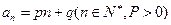 . 数列
. 数列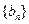 定义如下:对于正整数m,
定义如下:对于正整数m,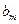 是使得不等式
是使得不等式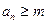 成立的所有n中的最小值.
成立的所有n中的最小值.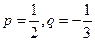 ,求
,求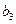 ;
;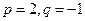 ,求数列
,求数列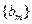 的前2m项和公式;
的前2m项和公式;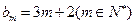 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.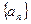 的前n项和为
的前n项和为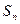 ,且
,且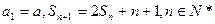
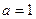 ,
,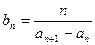 ,
,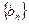 的前n项和为
的前n项和为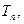 已知
已知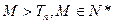 ,求M的最小值.
,求M的最小值.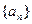 的前
的前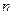 项和
项和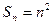 ,则
,则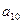 = ____________.
= ____________.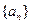 中,
中,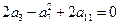 ,数列
,数列 是等比数列,且
是等比数列,且
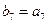 ,则
,则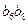 =" " ( ※ )
=" " ( ※ ) 中,
中, ,
, 则
则