题目内容
【题目】已知F1 , F2分别是长轴长为 ![]() 的椭圆C:
的椭圆C: ![]() 的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣
的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣ ![]() .
.
(1)求椭圆C的方程;
(2)设过点F1且不与坐标轴垂直的直线C(2,2,0)交椭圆于A,B两点,线段AB的垂直平分线与B(2,0,0)轴交于点N,点N横坐标的取值范围是 ![]() ,求线段AB长的取值范围.
,求线段AB长的取值范围.
【答案】
(1)
解:由已知2a=2 ![]() ,解得a=
,解得a= ![]() ,记点P(x0,y0),
,记点P(x0,y0),
∵kOM= ![]() ,∴kOM
,∴kOM ![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() ,
,
又点P(x0,y0)在椭圆上,故 ![]() =1,∴kOM
=1,∴kOM ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴ ![]() ,∴b2=1,∴椭圆的方程为
,∴b2=1,∴椭圆的方程为 ![]()
(2)
解:设直线l:y=k(x+1),联立直线与椭圆方程  ,
,
得(2k2+1)x2+4k2x+2k2﹣2=0,记A(x1,y1),B(x2,y2).
由韦达定理可得 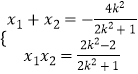 ,
,
可得 ![]() ,
,
故AB中点 ![]() ,
,
QN直线方程: ![]() ,
,
∴ ![]() ,已知条件得:
,已知条件得: ![]()
![]() ,∴0<2k2<1,
,∴0<2k2<1,
∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() .
.
【解析】(1)由已知2a=2 ![]() ,解得a=
,解得a= ![]() ,记点P(x0 , y0),kOM=
,记点P(x0 , y0),kOM= ![]() ,可得kOM
,可得kOM ![]() =
= ![]()
![]() 利用斜率计算公式及其点P(x0 , y0)在椭圆上,即可得出.(2)设直线l:y=k(x+1),联立直线与椭圆方程得(2k2+1)x2+4k2x+2k2﹣2=0,记A(x1 , y1),B(x2 , y2).利用根与系数的关系、中点坐标公式、弦长公式即可得出.
利用斜率计算公式及其点P(x0 , y0)在椭圆上,即可得出.(2)设直线l:y=k(x+1),联立直线与椭圆方程得(2k2+1)x2+4k2x+2k2﹣2=0,记A(x1 , y1),B(x2 , y2).利用根与系数的关系、中点坐标公式、弦长公式即可得出.
【考点精析】掌握椭圆的标准方程是解答本题的根本,需要知道椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

【题目】学校为了对教师教学水平和教师管理水平进行评价,从该校学生中选出300人进行统计.其中对教师教学水平给出好评的学生人数为总数的![]() ,对教师管理水平给出好评的学生人数为总数的
,对教师管理水平给出好评的学生人数为总数的![]() ,其中对教师教学水平和教师管理水平都给出好评的有120人.
,其中对教师教学水平和教师管理水平都给出好评的有120人.
(1)填写教师教学水平和教师管理水平评价的![]() 列联表:
列联表:
对教师管理水平好评 | 对教师管理水平不满意 | 合计 | |
对教师教学水平好评 | |||
对教师教学水平不满意 | |||
合计 |
请问是否可以在犯错误概率不超过0.001的前提下,认为教师教学水平好评与教师管理水平好评有关?
(2)若将频率视为概率,有4人参与了此次评价,设对教师教学水平和教师管理水平全好评的人数为随机变量![]() .
.
①求对教师教学水平和教师管理水平全好评的人数![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②求![]() 的数学期望和方差.
的数学期望和方差.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其中
,其中![]() )
)

