题目内容
【题目】如图所示,某街道居委会拟在![]() 地段的居民楼正南方向的空白地段
地段的居民楼正南方向的空白地段![]() 上建一个活动中心,其中
上建一个活动中心,其中![]() 米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形
米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形![]() ,上部分是以
,上部分是以![]() 为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长
为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长![]() 不超过
不超过![]() 米,其中该太阳光线与水平线的夹角
米,其中该太阳光线与水平线的夹角![]() 满足
满足![]() .
.

(1)若设计![]() 米,
米,![]() 米,问能否保证上述采光要求?
米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计![]() 与
与![]() 的长度,可使得活动中心的截面面积最大?(注:计算中
的长度,可使得活动中心的截面面积最大?(注:计算中![]() 取3)
取3)
【答案】(Ⅰ)能(Ⅱ)![]() 米且
米且![]() 米
米
 【解析】
【解析】
试题分析:(Ⅰ)由条件知研究直线与圆相切,所以建立坐标系:以点A为坐标原点,AB所在直线为x轴,,确定圆的方程,求出切线方程![]() ,解出切线与直线交点,最后判断
,解出切线与直线交点,最后判断![]() 是否满足不超过
是否满足不超过![]() 米这个条件(Ⅱ)同(1)建立坐标系,设立圆的方程:圆心为
米这个条件(Ⅱ)同(1)建立坐标系,设立圆的方程:圆心为![]() ,半径为
,半径为![]() ,求出切线方程
,求出切线方程![]() ,解出切线与直线交点,根据
,解出切线与直线交点,根据 ![]() 不超过
不超过![]() 米这个条件列参数限制条件
米这个条件列参数限制条件![]() ,最后根据活动中心的截面面积关系式求最值:
,最后根据活动中心的截面面积关系式求最值:![]()
![]()
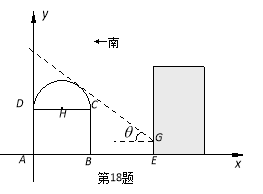
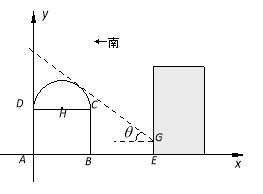
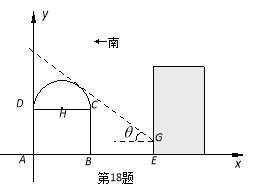
试题解析:解:如图所示,以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系.
(1)因为![]() ,
,![]() ,所以半圆的圆心为
,所以半圆的圆心为![]() ,
,
半径![]() .设太阳光线所在直线方程为
.设太阳光线所在直线方程为![]() ,
,
即![]() , ...............2分
, ...............2分
则由![]() ,
,
 解得
解得![]() 或
或![]() (舍).
(舍).
故太阳光线所在直线方程为![]() , ...............5分
, ...............5分
令![]() ,得
,得![]() 米
米![]() 米.
米.
所以此时能保证上述采光要求. ...............7分
(2)设![]() 米,
米,![]() 米,则半圆的圆心为
米,则半圆的圆心为![]() ,半径为
,半径为![]() .
.
方法一:设太阳光线所在直线方程为![]() ,
,
即![]() ,由
,由![]() ,
,
解得![]() 或
或![]() (舍). ...............9分
(舍). ...............9分
故太阳光线所在直线方程为![]() ,
,
令![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() . ...............11分
. ...............11分
所以![]()
![]() .
.
当且仅当![]() 时取等号.
时取等号.
所以当![]() 米且
米且![]() 米时,可使得活动中心的截面面积最大. .............16分
米时,可使得活动中心的截面面积最大. .............16分
方法二:欲使活动中心内部空间尽可能大,则影长EG恰为![]() 米,则此时点
米,则此时点![]() 为
为![]() ,
,
设过点G的上述太阳光线为![]() ,则
,则![]() 所在直线方程为y-=-(x-30),
所在直线方程为y-=-(x-30),
即![]() . ........10分
. ........10分
由直线![]() 与半圆H相切,得
与半圆H相切,得![]() .
.
而点H(r,h)在直线![]() 的下方,则3r+4h-100<0,
的下方,则3r+4h-100<0,
即![]() ,从而
,从而![]() . ...............13分
. ...............13分
又![]()
![]() .
.
当且仅当![]() 时取等号.
时取等号.
所以当![]() 米且
米且![]() 米时,可使得活动中心的截面面积最大. ...........16分
米时,可使得活动中心的截面面积最大. ...........16分





