题目内容
【题目】设数列A:![]() ,
,![]() ,…
,…![]() (
(![]() ).如果对小于
).如果对小于![]() (
(![]() )的每个正整数
)的每个正整数![]() 都有
都有![]() <
<![]() ,则称
,则称![]() 是数列A的一个“G时刻”.记“
是数列A的一个“G时刻”.记“![]() 是数列A的所有“G时刻”组成的集合.
是数列A的所有“G时刻”组成的集合.
(1)对数列A:-2,2,-1,1,3,写出![]() 的所有元素;
的所有元素;
(2)证明:若数列A中存在![]() 使得
使得![]() >
>![]() ,则
,则![]() ;
;
(3)证明:若数列A满足![]() -
-![]() ≤1(n=2,3, …,N),则
≤1(n=2,3, …,N),则![]() 的元素个数不小于
的元素个数不小于![]() -
-![]() .
.
【答案】(1)![]() 的元素为
的元素为![]() 和
和![]() ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
试题(Ⅰ)关键是理解“G时刻”的定义,根据定义即可写出![]() 的所有元素;
的所有元素;
(Ⅱ)要证![]() ,即证
,即证![]() 中含有一元素即可;
中含有一元素即可;
(Ⅲ)当![]() 时,结论成立.只要证明当
时,结论成立.只要证明当![]() 时结论仍然成立即可.
时结论仍然成立即可.
试题解析:(Ⅰ)![]() 的元素为
的元素为![]() 和
和![]() .
.
(Ⅱ)因为存在![]() 使得
使得![]() ,所以
,所以![]() .
.
记![]() ,
,
则![]() ,且对任意正整数
,且对任意正整数![]() .
.
因此![]() ,从而
,从而![]() .
.
(Ⅲ)当![]() 时,结论成立.
时,结论成立.
以下设![]() .
.
由(Ⅱ)知![]() .
.
设![]() .记
.记![]() .
.
则![]() .
.
对![]() ,记
,记![]() .
.
如果![]() ,取
,取![]() ,则对任何
,则对任何![]() .
.
从而![]() 且
且![]() .
.
又因为![]() 是
是![]() 中的最大元素,所以
中的最大元素,所以![]() .
.
从而对任意![]() ,
,![]() ,特别地,
,特别地,![]() .
.
对![]() .
.
因此![]() .
.
所以![]() .
.
因此![]() 的元素个数p不小于
的元素个数p不小于![]() .
.

【题目】大学的生活丰富多彩,很多学生除了学习本专业的必修课外,还会选择一些选修课来充实自已.甲同学调查了自己班上的![]() 名同学学习选修课的情况,并作出如下表格:
名同学学习选修课的情况,并作出如下表格:
每人选择选修课科数 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)求甲同学班上人均学习选修课科数:
(2)甲同学和乙同学的某门选修课是在同一个班,且该门选修课开始上课的时间是早上![]() ,已知甲同学每次上课都会在
,已知甲同学每次上课都会在![]() 到
到![]() 之间的任意时刻到达教室,乙同学每次上课都会在
之间的任意时刻到达教室,乙同学每次上课都会在![]() 到
到![]() 之间的任意时刻到达教室,求连续
之间的任意时刻到达教室,求连续![]() 天内,甲同学比乙同学早到教室的天数
天内,甲同学比乙同学早到教室的天数![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.新能源汽车销售的春天来了!从衡阳地区某品牌新能源汽车销售公司了解到,为了帮助品牌迅速占领市场,他们采取了保证公司正常运营的前提下实行薄利多销的营销策略(即销售单价随日销量![]() (台)变化而有所变化),该公司的日盈利
(台)变化而有所变化),该公司的日盈利![]() (万元),经过一段时间的销售得到
(万元),经过一段时间的销售得到![]() ,
,![]() 的一组统计数据如下表:
的一组统计数据如下表:
日销量 | 1 | 2 | 3 | 4 | 5 |
日盈利 | 6 | 13 | 17 | 20 | 22 |
将上述数据制成散点图如图所示:
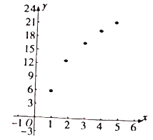
(1)根据散点图判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() ,
,![]() 之间的关系?并从函数增长趋势方面给出简单的理由;
之间的关系?并从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并预测当日销量
的回归方程,并预测当日销量![]() 时,日盈利是多少?
时,日盈利是多少?
参考公式及数据:线性回归方程![]() ,其中
,其中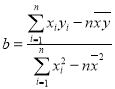 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,![]() .
.