题目内容
(本小题满分12分)
如图6,已知正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1。
(1)求证:平面AB1D⊥平面B1BCC1;
(2)求证:A1C//平面AB1D;
(3)求二面角B—AB1—D的正切值。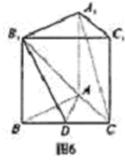
如图6,已知正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1。
(1)求证:平面AB1D⊥平面B1BCC1;
(2)求证:A1C//平面AB1D;
(3)求二面角B—AB1—D的正切值。

(1)证明见解析。
(2)证明见解析。
(3)二面角B—AB1—D的正切值为
(2)证明见解析。
(3)二面角B—AB1—D的正切值为

解法一:
证明:(
 1)因为B1B⊥平面ABC,AD
1)因为B1B⊥平面ABC,AD 平面ABC,
平面ABC,所以AD⊥B1B (1分)
因为D为正△ABC中BC的中点,
所以AD⊥BD (2分)
又B1B∩BC=B,
所以AD⊥平面B1BCC1 (3分)
又AD
 平面AB1D,故平面AB1D⊥平面B1BCC1 (4分)
平面AB1D,故平面AB1D⊥平面B1BCC1 (4分)(2)连接A1B,交AB1于E,连DE (5分)
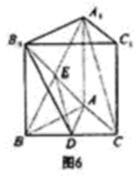
因为点E为矩形A1ABB1对角线的交点,所以E为AB1的中点 (6分)
又D为BC
 的中点,所以DE为△A1BC的中位线,
的中点,所以DE为△A1BC的中位线,所以DE//A1C (7分)
又DE
 平面AB1D,所以A1C//平面AB1D (8分)
平面AB1D,所以A1C//平面AB1D (8分)(3)解:过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG。
因为平面A1ABB1⊥平面ABC,DF⊥AB,所以DF⊥平面A1ABB1。
又AB1
 平面A1ABB1,所以AB1⊥DF。
平面A1ABB1,所以AB1⊥DF。又FG⊥AB1,所以AB1⊥平面DFG,所以AB1⊥DG。 (9分)
又AB1⊥FG,所以∠DGF为
 二面角B—AB1—D的平面角。 (10分)
二面角B—AB1—D的平面角。 (10分)因为AA1=AB=1,
所以在正△ABC中,

在
 (11分)
(11分)所以在
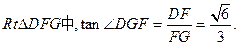 (12分)
(12分)解法二:
解:建立如图所示的直角坐标系,依题意有:

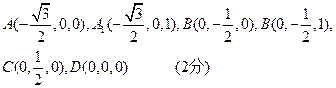
(1)证明:由
 ,
,得
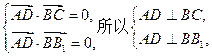
又BC∩⊥BB1=B,所以AD⊥平面B1BCC1。 (4分)
又AD
 平面AB1D,所以平面AB1D⊥B1BCC1 (5分)
平面AB1D,所以平面AB1D⊥B1BCC1 (5分)(2)证明:连接A1B,交AB1于E,连DE,
因为点E为正方形A1ABB1对角线的交点,所以E为AB1的中点,
即
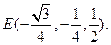 (6分)
(6分)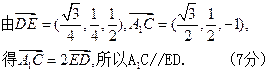
又DE
 平面AB1D,所以A1C//平面AB1D (8分)
平面AB1D,所以A1C//平面AB1D (8分)(3)解:设平面ABB1的一个法向量为
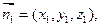
由
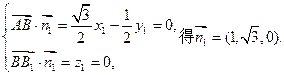 (9分)
(9分)设平面AB1D的一个法向量为
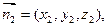
由
 (10分)
(10分)所以
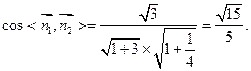 (11分)
(11分)所以
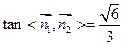 ,
,依图可得二面角B—AB1—D的正切值为
 (12分)
(12分)
练习册系列答案
相关题目
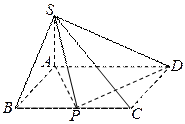 如图,四棱锥
如图,四棱锥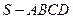 的底面是矩形,
的底面是矩形,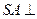 底面
底面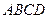 ,P为BC边的中点,SB与
,P为BC边的中点,SB与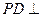 平面SAP;
平面SAP;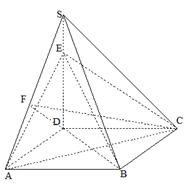 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.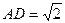 ,E是SD上的点.(Ⅰ)求证:AC⊥BE;
,E是SD上的点.(Ⅰ)求证:AC⊥BE;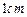 的正方体。
的正方体。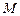 、
、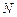 、
、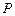 、
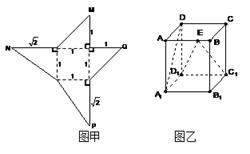
、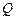 重合,则可以围成怎样的几何体?请求出此几何体的体积;
重合,则可以围成怎样的几何体?请求出此几何体的体积; 体?请按图乙中所标字母写出这几个几何体的名称;
体?请按图乙中所标字母写出这几个几何体的名称;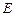 为棱
为棱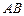 上的动点,试判断
上的动点,试判断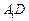 与平面
与平面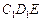 是否垂直,并说明理由。
是否垂直,并说明理由。

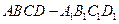 中,
中, 分别是
分别是 的中点.
的中点. 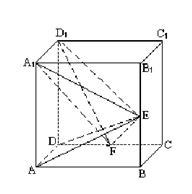
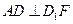 ; (2)求
; (2)求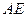 与
与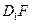 所成的角;
所成的角;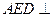 面
面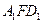 ;(4)
;(4)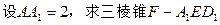 的体积
的体积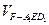
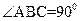 ,
,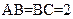 ,二面角P-AB-C为
,二面角P-AB-C为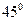 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.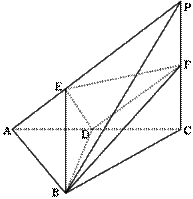
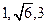 ,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。
,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。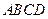 --
--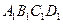 ,E、F分别是
,E、F分别是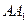 、
、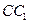 的中点,p是
的中点,p是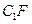 B、线段
B、线段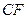 C、线段
C、线段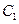 D、线段
D、线段