题目内容
14.已知函数f(x)=2sin2x+2sin22x+cos4x.(Ⅰ)求f(x)的最小正周期;
(Ⅱ)若$g(x)=f(x+φ),(-\frac{π}{2}<φ<\frac{π}{2})$在x=$\frac{π}{3}$处取得最大值,求φ的值;
(Ⅲ)在(Ⅱ)的条件下,求y=g(x)的单调递增区间.
分析 (Ⅰ)利用二倍角公式对函数解析式化简,利用周期公式求得最小正周期.
(Ⅱ)先求得g(x)的表达式,推断在取得最大值时,表达式$\frac{π}{3}$.
(Ⅲ)确定g(x)的解析式,根据三角函数图象与性质求得单调区间.
解答 解:(Ⅰ) f(x)=2sin2x+1-cos4x+cos4x=2sin2x+1,
所以T=$\frac{2π}{2}$=π.
(Ⅱ)g(x)=f(x+φ)=2sin(2x+2φ)+1,
当2x+2φ=$\frac{π}{2}$+2kπ,k∈Z时取得最大值,将x=$\frac{π}{3}$代入上式,
解得φ=-$\frac{π}{12}$+kπ,k∈Z,
∵-$\frac{π}{2}$<φ<$\frac{π}{2}$,∴φ=-$\frac{π}{12}$.
(Ⅲ)由(Ⅱ)知,g(x)=2sin(2x-$\frac{π}{6}$)+1,
又-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,
解得-$\frac{π}{6}$+kπ≤x≤$\frac{π}{3}$+kπ,
∴函数g(x)的单调递增区间为:[-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ,](k∈Z).
点评 本题主要考查了三角函数的图象与性质;三角函数的单调性,三角函数的最值、和角公式和二倍角公式.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
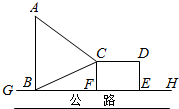 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm