题目内容
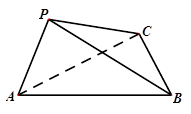
如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点, 那么异面直线EF与SA所成的角等于 ( )


| A.60° | B.90° | C.45° | D.30 |
C
解:
取AC中点G,连接EG,GF,FC
设棱长为2,则CF=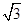 ,而CE=1
,而CE=1
∴EF=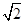 ,GE=1,GF=1
,GE=1,GF=1
而GE∥SA,∴∠GEF为异面直线EF与SA所成的角
∵EF=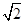 ,GE=1,GF=1
,GE=1,GF=1
∴△GEF为等腰直角三角形,故∠GEF=45°
故选C
取AC中点G,连接EG,GF,FC
设棱长为2,则CF=
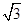 ,而CE=1
,而CE=1∴EF=
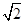 ,GE=1,GF=1
,GE=1,GF=1而GE∥SA,∴∠GEF为异面直线EF与SA所成的角
∵EF=
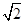 ,GE=1,GF=1
,GE=1,GF=1∴△GEF为等腰直角三角形,故∠GEF=45°
故选C

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 平面AEB,
平面AEB, ,
, ,
, ,
, ,
, ,
, ,G是BC的中点.
,G是BC的中点.
 ;
; 的大小.
的大小.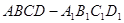 中.
中.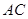 与
与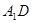 所成角的大小;
所成角的大小;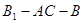 的正切值.
的正切值.
 中,
中, 分别是棱
分别是棱 的中点,则直线
的中点,则直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 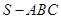 中,各个面都是边长为
中,各个面都是边长为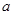 的正三角形,
的正三角形,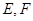 分别是
分别是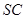 和
和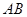 的中 点,则异面直线
的中 点,则异面直线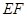 与
与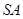 所成的角等于( )
所成的角等于( )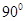 B
B 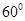 C
C 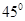 D
D 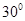
 棱BB1、AD的中点,则直线EF和平面
棱BB1、AD的中点,则直线EF和平面 所成的角的正弦值是( )
所成的角的正弦值是( )




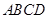 ,
,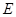 是
是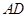 中点,则直线
中点,则直线 与直线
与直线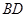 所成的角的余弦值为( )
所成的角的余弦值为( ) 



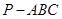 中,
中,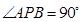 ,
,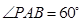 ,
,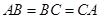 ,平面
,平面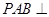 平面
平面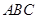 。
。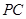 与平面
与平面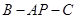 的大小。
的大小。