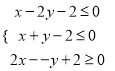Question

【题目】已知命题p：“x∈[1，2]， x2－lnx－a≥0”与命题q：“x∈R，x2＋2ax－8－6a＝0”都是真命题，求实数a的取值范围．

Answer 1

【答案】 (－∞，－4]∪[－2，]

【解析】

根据题意，命题p，利用恒成立问题方法转化，求出a的取值范围；

命题q，由一元二次方程的根的情况分析可得a的取值范围，根据p、q都是真命题，将两次求出的a的范围求交集即可.

命题p：a≤x2－lnx在x∈[1，2]上恒成立，令f(x)＝x2－lnx，f ′(x)＝x-＝ ，

当1<x<2时，f′(x)>0，∴f(x)min＝f(1)＝.∴a≤. 即：当a≤时，p是真命题.，

命题q：Δ＝4a2－4(－8－6a)≥0，∴a≥－2或a≤－4.即当 a≥－2或a≤－4时，q是真命题，

综上，a的取值范围为(－∞，－4]∪[－2，]．