Question

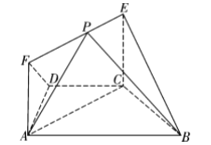
【题目】如图，四边形ABCD是棱长为2的正方形，E为AD的中点，以CE为折痕把△DEC折起，使点D到达点P的位置，且点P的射影O落在线段AC上．

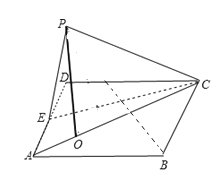
（1）求；

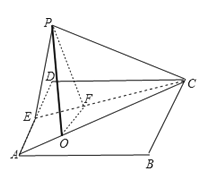
（2）求几何体P﹣ABCE的体积．

Answer 1

【答案】（1）2（2）．

【解析】

（1）由题得平面，过点P作PF⊥CE于F，连接FO，则OF⊥CE，在中，求得，即得解；（2）利用几何体的体积求解.

（1）由题得平面，

过点P作PF⊥CE于F，连接FO，则OF⊥CE，

在Rt△PEC中，PE＝1，PC＝2，则EC，

PF，

CF，

在△AEC中，

cos∠ACE，

在Rt△OFC中，CO，

∴AO＝AC﹣CO＝2，

∴2．

（2）在Rt△OFC中，

OF，∴PO，

SABCE＝SABCD﹣S△DEC＝2×23，

∴几何体P﹣ABCE的体积：

V．