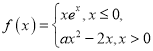题目内容
【题目】已知数列{an}中,a1=0,an+1=an+6n+3,数列{bn}满足bn=n![]() ,则数列{bn}的最大项为第_____项
,则数列{bn}的最大项为第_____项
【答案】11
【解析】
首先利用叠加法求出数列的通项公式,进一步利用数列的单调性的应用求出数列的最大项.
数列{an}中,a1=0,an+1=an+6n+3,则an+1﹣an=6n+3,整理得an﹣an﹣1=6(n﹣1)+3,…a2﹣a1=6×1+3,
利用叠加法得到an﹣a1=6(1+2+…+n﹣1)+3(n﹣1),解得an=3(n﹣1)(n+1),故![]() ,
,
所以足bn=n![]() .
.
![]() 即
即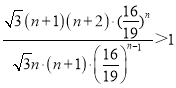 ,整理得
,整理得![]() ,
,
即![]() ,当
,当![]() n≥1时,bn单调递增,当
n≥1时,bn单调递增,当![]() 时,单调递减,
时,单调递减,
n=10时,b10=110![]() (
(![]() )9,n=11时,b11=132
)9,n=11时,b11=132![]() (
(![]() )10,
)10,
![]() 1,即b11>b10,
1,即b11>b10,
故当n=11时,数列{bn}存在最大项为第11项.

练习册系列答案
相关题目
【题目】某市推行“共享汽车”服务,租用汽车按行驶里程加用车时间收费,标准是“1元/公里+0.2元/分钟”,刚在该市参加工作的小刘拟租用“共享汽车“上下班.单位同事老李告诉他:“上下班往返总路程虽然只有10公里,但偶尔上下班总共也需要用时大约1小时”,并将自己近50天往返开车的花费时间情况统计如下
时间(分钟) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
次数ξ | 8 | 18 | 14 | 8 | 2 |
将老李统计的各时间段频率视为相应概率,假定往返的路况不变,而且每次路上开车花费时间视为用车时间.
(1)试估计小刘每天平均支付的租车费用(每个时间段以中点时间计算);
(2)小刘认为只要上下班开车总用时不超过45分钟,租用“共享汽车”为他该日的“最优选择”,小刘拟租用该车上下班2天,设其中有ξ天为“最优选择”,求ξ的分布列和数学期望.