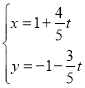ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥Τϊ≥ΒΝψΦΰΦ”ΙΛ≥ßΈΣ”≠Ϋ”Ιζ«λ¥σ¥ΌœζΜνΕ·‘ΛΙάΙζ«λΤΏΧλœζ έΝΩΘ§ΗΟ≥ßΙΛΉς»Υ‘±ΗυΨί“‘ΆυΗΟ≥ßΒΡœζ έ«ιΩωΘ§Μφ÷ΤΝΥΗΟ≥ß»’œζ έΝΩΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§»γΆΦΥυ ΨΘ§ΫΪ»’œζ έΝΩ¬δ»κΗςΉιΒΡΤΒ¬ ”ΈΣΗ≈¬ Θ§≤ΔΦΌ…ηΟΩΧλΒΡœζ έΝΩœύΜΞΕάΝΔ.
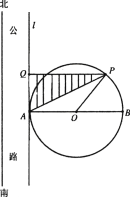
Θ®1Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΙάΦΤΗΟ≥ßΒΡ»’ΤΫΨυœζ έΝΩΘΜ(ΟΩΉι“‘÷–Βψ÷ΒΈΣ¥ζ±μ)
Θ®2Θ©«σΈ¥ά¥![]() ΧλΡΎΘ§Ν§–χ
ΧλΡΎΘ§Ν§–χ![]() Χλ»’œζ έΝΩ≤ΜΒΆ”Ύ
Χλ»’œζ έΝΩ≤ΜΒΆ”Ύ![]() Ε÷Θ§Νμ“ΜΧλ»’œζ έΝΩΒΆ”Ύ
Ε÷Θ§Νμ“ΜΧλ»’œζ έΝΩΒΆ”Ύ![]() Ε÷ΒΡΗ≈¬ ΘΜ
Ε÷ΒΡΗ≈¬ ΘΜ
Θ®3Θ©”Ο![]() ±μ ΨΈ¥ά¥
±μ ΨΈ¥ά¥![]() ΧλΡΎ»’œζ έΝΩ≤ΜΒΆ”Ύ
ΧλΡΎ»’œζ έΝΩ≤ΜΒΆ”Ύ![]() Ε÷ΒΡΧλ ΐΘ§«σΥφΜζ±δΝΩ
Ε÷ΒΡΧλ ΐΘ§«σΥφΜζ±δΝΩ![]() ΒΡΖ÷≤ΦΝ–ΓΔ ΐ―ßΤΎΆϊ”κΖΫ≤ν.
ΒΡΖ÷≤ΦΝ–ΓΔ ΐ―ßΤΎΆϊ”κΖΫ≤ν.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ®Ε÷Θ©ΘΜΘ®2Θ©
Θ®Ε÷Θ©ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©ΥφΜζ±δΝΩ
ΘΜΘ®3Θ©ΥφΜζ±δΝΩ![]() ΒΡΖ÷≤ΦΝ–»γœ¬ΆΦΥυ ΨΘΚ
ΒΡΖ÷≤ΦΝ–»γœ¬ΆΦΥυ ΨΘΚ
X | 0 | 1 | 2 | 3 |
P | 0.027 | 0.189 | 0.441 | 0.343 |
ΥφΜζ±δΝΩ![]() ΒΡ ΐ―ßΤΎΆϊΈΣΘΚ
ΒΡ ΐ―ßΤΎΆϊΈΣΘΚ![]()
ΥφΜζ±δΝΩ![]() ΒΡΖΫ≤νΈΣΘΚ
ΒΡΖΫ≤νΈΣΘΚ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί“―÷ΣΫαΚœΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΫχ––«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©Έ¥ά¥![]() ΧλΡΎΘ§Ν§–χ
ΧλΡΎΘ§Ν§–χ![]() Χλ»’œζ έΝΩ≤ΜΒΆ”Ύ
Χλ»’œζ έΝΩ≤ΜΒΆ”Ύ![]() Ε÷Θ§Νμ“ΜΧλ»’œζ έΝΩΒΆ”Ύ
Ε÷Θ§Νμ“ΜΧλ»’œζ έΝΩΒΆ”Ύ![]() Ε÷Θ§”–Εΰ÷÷«ι–ΈΘΚ“Μ «ΒΎ“ΜΧλΓΔΒΎΕΰΧλœζ έΝΩ≤ΜΒΆ”Ύ
Ε÷Θ§”–Εΰ÷÷«ι–ΈΘΚ“Μ «ΒΎ“ΜΧλΓΔΒΎΕΰΧλœζ έΝΩ≤ΜΒΆ”Ύ![]() Ε÷Θ§ΒΎ»ΐΧλœζ έΝΩΒΆ”Ύ
Ε÷Θ§ΒΎ»ΐΧλœζ έΝΩΒΆ”Ύ![]() Ε÷ΘΜΕΰ «ΒΎ“ΜΧλœζ έΝΩΒΆ”Ύ
Ε÷ΘΜΕΰ «ΒΎ“ΜΧλœζ έΝΩΒΆ”Ύ![]() Ε÷Θ§ΒΎΕΰΧλΓΔΒΎ»ΐœζ έΝΩ≤ΜΒΆ”Ύ
Ε÷Θ§ΒΎΕΰΧλΓΔΒΎ»ΐœζ έΝΩ≤ΜΒΆ”Ύ![]() Ε÷Θ§‘ΥΥψΚΆ ¬ΦΰΒΡΗ≈¬ ΦΤΥψΙΪ ΫΫχ––«σΫβΦ¥Ω…ΘΜ
Ε÷Θ§‘ΥΥψΚΆ ¬ΦΰΒΡΗ≈¬ ΦΤΥψΙΪ ΫΫχ––«σΫβΦ¥Ω…ΘΜ
Θ®3Θ©Ω…“‘≈–Εœ≥ωΥφΜζ±δΝΩ![]() Ζΰ¥”ΕΰœνΖ÷≤ΦΘ§ΗυΨίΕΰœνΖ÷≤ΦΒΡ–‘÷ Ϋχ––«σΫβΦ¥Ω….
Ζΰ¥”ΕΰœνΖ÷≤ΦΘ§ΗυΨίΕΰœνΖ÷≤ΦΒΡ–‘÷ Ϋχ––«σΫβΦ¥Ω….
Θ®1Θ©ΗΟ≥ßΒΡ»’ΤΫΨυœζ έΝΩΈΣΘΚ
![]() Θ®Ε÷Θ©ΘΜ
Θ®Ε÷Θ©ΘΜ
Θ®2Θ©»’œζ έΝΩΒΆ”Ύ![]() Ε÷ΒΡΗ≈¬ ΈΣΘΚ
Ε÷ΒΡΗ≈¬ ΈΣΘΚ![]() Θ§
Θ§
‘ρ»’œζ έΝΩ≤ΜΒΆ”Ύ![]() Ε÷ΒΡΗ≈¬ ΈΣΘΚ
Ε÷ΒΡΗ≈¬ ΈΣΘΚ![]() .
.
Υυ“‘Έ¥ά¥![]() ΧλΡΎΘ§Ν§–χ
ΧλΡΎΘ§Ν§–χ![]() Χλ»’œζ έΝΩ≤ΜΒΆ”Ύ
Χλ»’œζ έΝΩ≤ΜΒΆ”Ύ![]() Ε÷Θ§Νμ“ΜΧλ»’œζ έΝΩΒΆ”Ύ
Ε÷Θ§Νμ“ΜΧλ»’œζ έΝΩΒΆ”Ύ![]() Ε÷ΒΡΗ≈¬ ΈΣΘΚ
Ε÷ΒΡΗ≈¬ ΈΣΘΚ
![]() ΘΜ
ΘΜ
Θ®3Θ©”…Θ®2Θ©Ω…÷ΣΘΚ»’œζ έΝΩ≤ΜΒΆ”Ύ![]() Ε÷ΒΡΗ≈¬ ΈΣΘΚ
Ε÷ΒΡΗ≈¬ ΈΣΘΚ![]() .”…Χβ“βΩ…÷ΣΘΚΥφΜζ±δΝΩ
.”…Χβ“βΩ…÷ΣΘΚΥφΜζ±δΝΩ![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ
ΒΡΩ…Ρή»Γ÷ΒΈΣ![]() Θ§«“
Θ§«“![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() .
.
ΥφΜζ±δΝΩ![]() ΒΡΖ÷≤ΦΝ–»γœ¬ΆΦΥυ ΨΘΚ
ΒΡΖ÷≤ΦΝ–»γœ¬ΆΦΥυ ΨΘΚ
X | 0 | 1 | 2 | 3 |
P | 0.027 | 0.189 | 0.441 | 0.343 |
ΥφΜζ±δΝΩ![]() ΒΡ ΐ―ßΤΎΆϊΈΣΘΚ
ΒΡ ΐ―ßΤΎΆϊΈΣΘΚ![]()
ΥφΜζ±δΝΩ![]() ΒΡΖΫ≤νΈΣΘΚ
ΒΡΖΫ≤νΈΣΘΚ![]()

 ΨΌ“ΜΖ¥»ΐΒΞ‘ΣΆ§≤ΫΙΐΙΊΨμœΒΝ–¥πΑΗ
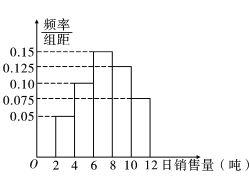
ΨΌ“ΜΖ¥»ΐΒΞ‘ΣΆ§≤ΫΙΐΙΊΨμœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥≥« –ΒΡΙΪΫΜΙΪΥΨΈΣΝΥΖΫ±ψ –Οώ≥ω––Θ§ΩΤ―ßΙφΜ°≥ΒΝΨΆΕΖ≈Θ§‘Ύ“ΜΗω»Υ‘±ΟήΦ·ΝςΕ·ΒΊΕΈ‘ω…η“ΜΗωΤπΒψ’ΨΘ§ΈΣΝΥ―–ΨΩ≥ΒΝΨΖΔ≥ΒΦδΗτ ±Φδ![]() ”κ≥ΥΩΆΒ»Κρ»Υ ΐ
”κ≥ΥΩΆΒ»Κρ»Υ ΐ![]() ÷°ΦδΒΡΙΊœΒΘ§Ψ≠ΙΐΒς≤ιΒΟΒΫ»γœ¬ ΐΨίΘΚ
÷°ΦδΒΡΙΊœΒΘ§Ψ≠ΙΐΒς≤ιΒΟΒΫ»γœ¬ ΐΨίΘΚ
ΦδΗτ ±Φδ/Ζ÷ | 10 | 11 | 12 | 13 | 14 | 15 |
Β»Κρ»Υ ΐy/»Υ | 23 | 25 | 26 | 29 | 28 | 31 |
Βς≤ι–ΓΉιœ»¥”’β![]() Ήι ΐΨί÷–―Γ»Γ
Ήι ΐΨί÷–―Γ»Γ![]() Ήι ΐΨί«σœΏ–‘ΜΊΙιΖΫ≥ΧΘ§‘Ό”Ο Θœ¬ΒΡ
Ήι ΐΨί«σœΏ–‘ΜΊΙιΖΫ≥ΧΘ§‘Ό”Ο Θœ¬ΒΡ![]() Ήι ΐΨίΫχ––Φλ―ιΘ°Φλ―ιΖΫΖ®»γœ¬ΘΚœ»”Ο«σΒΟΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΦΤΥψΦδΗτ ±ΦδΕ‘”ΠΒΡΒ»Κρ»Υ ΐ
Ήι ΐΨίΫχ––Φλ―ιΘ°Φλ―ιΖΫΖ®»γœ¬ΘΚœ»”Ο«σΒΟΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΦΤΥψΦδΗτ ±ΦδΕ‘”ΠΒΡΒ»Κρ»Υ ΐ![]() Θ§‘Ό«σ
Θ§‘Ό«σ![]() ”κ ΒΦ Β»Κρ»Υ ΐ
”κ ΒΦ Β»Κρ»Υ ΐ![]() ΒΡ≤νΘ§»τ≤ν÷ΒΒΡΨχΕ‘÷ΒΕΦ≤Μ≥§Ιΐ
ΒΡ≤νΘ§»τ≤ν÷ΒΒΡΨχΕ‘÷ΒΕΦ≤Μ≥§Ιΐ![]() Θ§‘ρ≥ΤΥυ«σΖΫ≥Χ «ΓΑ«ΓΒ±ΜΊΙιΖΫ≥ΧΓ±Θ°
Θ§‘ρ≥ΤΥυ«σΖΫ≥Χ «ΓΑ«ΓΒ±ΜΊΙιΖΫ≥ΧΓ±Θ°
Θ®1Θ©¥”’β![]() Ήι ΐΨί÷–ΥφΜζ―Γ»Γ
Ήι ΐΨί÷–ΥφΜζ―Γ»Γ![]() Ήι ΐΨίΚσΘ§«σ Θœ¬ΒΡ
Ήι ΐΨίΚσΘ§«σ Θœ¬ΒΡ![]() Ήι ΐΨίΒΡΦδΗτ ±Φδ≤ΜœύΝΎΒΡΗ≈¬ ΘΜ
Ήι ΐΨίΒΡΦδΗτ ±Φδ≤ΜœύΝΎΒΡΗ≈¬ ΘΜ
Θ®2Θ©»τ―Γ»ΓΒΡ «ΚσΟφ![]() Ήι ΐΨίΘ§«σ
Ήι ΐΨίΘ§«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ
ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ![]() Θ§≤Δ≈–Εœ¥ΥΖΫ≥Χ «Ζώ «ΓΑ«ΓΒ±ΜΊΙιΖΫ≥ΧΓ±ΘΜ
Θ§≤Δ≈–Εœ¥ΥΖΫ≥Χ «Ζώ «ΓΑ«ΓΒ±ΜΊΙιΖΫ≥ΧΓ±ΘΜ
Θ®3Θ©ΈΣΝΥ ΙΒ»ΚρΒΡ≥ΥΩΆ≤Μ≥§Ιΐ![]() »ΥΘ§ ‘”ΟΘ®2Θ©÷–ΖΫ≥ΧΙάΦΤΦδΗτ ±ΦδΉνΕύΩ…“‘…η÷ΟΈΣΕύ…ΌΘ®ΨΪ»ΖΒΫ’ϊ ΐΘ©Ζ÷÷”Θ°
»ΥΘ§ ‘”ΟΘ®2Θ©÷–ΖΫ≥ΧΙάΦΤΦδΗτ ±ΦδΉνΕύΩ…“‘…η÷ΟΈΣΕύ…ΌΘ®ΨΪ»ΖΒΫ’ϊ ΐΘ©Ζ÷÷”Θ°
ΗΫΘΚΕ‘”Ύ“ΜΉι ΐΨί![]() Θ§
Θ§![]() Θ§Γ≠Γ≠Θ§
Θ§Γ≠Γ≠Θ§![]() Θ§ΤδΜΊΙι÷±œΏ
Θ§ΤδΜΊΙι÷±œΏ![]() ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΖ÷±πΈΣΘΚ
ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΖ÷±πΈΣΘΚ
 Θ§
Θ§![]() .
.