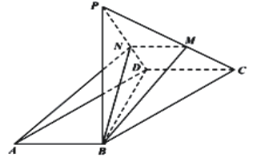
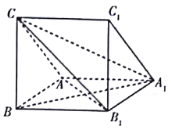
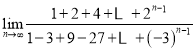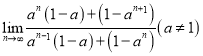ΧβΡΩΡΎ»ί
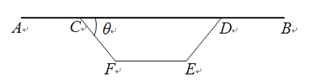
ΓΨΧβΡΩΓΩΆΦ1 «Ρ≥ΗΏΦή«≈œδΝΚΒΡΚαΫΊΟφΘ§Υϋ”……œ≤Ω¬ΖΟφΚΆœ¬≤Ω÷ß≥≈œδΝΫ≤ΩΖ÷Ήι≥…Θ°»γΆΦ2Θ§¬ΖΟφΩμΕ»![]() Θ§œ¬≤Ω÷ß≥≈œδCDEFΈΣΒ»―ϋΧί–ΈΘ®
Θ§œ¬≤Ω÷ß≥≈œδCDEFΈΣΒ»―ϋΧί–ΈΘ®![]() Θ©Θ§«“
Θ©Θ§«“![]() Θ°ΈΣΝΥ±Θ÷Λ≥–÷ΊΡήΝΠ”κΈ»Ε®–‘Θ§–ηœ¬≤Ω÷ß≥≈œδΒΡΟφΜΐΈΣ
Θ°ΈΣΝΥ±Θ÷Λ≥–÷ΊΡήΝΠ”κΈ»Ε®–‘Θ§–ηœ¬≤Ω÷ß≥≈œδΒΡΟφΜΐΈΣ![]() Θ§ΗΏΕ»ΈΣ2m«“
Θ§ΗΏΕ»ΈΣ2m«“![]() Θ§»τ¬ΖΟφABΘ°≤ύ±ΏCFΚΆDEΘ§ΒΉ≤ΩEFΒΡ‘λΦέΖ÷±πΈΣ4a«ß‘Σ/mΘ§5a«ß‘Σ/mΘ§6a«ß‘Σ/mΘ®aΈΣ’ΐ≥Θ ΐΘ©Θ§
Θ§»τ¬ΖΟφABΘ°≤ύ±ΏCFΚΆDEΘ§ΒΉ≤ΩEFΒΡ‘λΦέΖ÷±πΈΣ4a«ß‘Σ/mΘ§5a«ß‘Σ/mΘ§6a«ß‘Σ/mΘ®aΈΣ’ΐ≥Θ ΐΘ©Θ§![]() Θ°
Θ°

Θ®1Θ© ‘”ΟΠ»±μ ΨœδΝΚΒΡΉή‘λΦέyΘ®«ß‘ΣΘ©ΘΜ
Θ®2Θ© ‘»ΖΕ®cosΠ»ΒΡ÷ΒΘ§ ΙΉή‘λΦέΉνΒΆ?≤Δ«σΉνΒΆΉή‘λΦέΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() Θ§Τδ÷–
Θ§Τδ÷–![]() ΘΜΘ®2Θ©Β±
ΘΜΘ®2Θ©Β±![]() ΒΡ÷ΒΈΣ
ΒΡ÷ΒΈΣ![]() ±Θ§Ήή‘λΦέΉνΒΆΘ§ΈΣ
±Θ§Ήή‘λΦέΉνΒΆΘ§ΈΣ![]() «ß‘ΣΘ°
«ß‘ΣΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψFΉς![]() ”ΎΒψHΘ§”…»ΐΫ«Κ· ΐΦΑ÷ß≥≈ΟφΟφΜΐΩ…ΒΟ
”ΎΒψHΘ§”…»ΐΫ«Κ· ΐΦΑ÷ß≥≈ΟφΟφΜΐΩ…ΒΟ![]() Θ§–¥≥ωΉή‘λΦέ”κΠ»ΒΡΙΊœΒΘ§≤ΔΖ÷ΈωΚ· ΐΕ®“ε”ρΘΜ
Θ§–¥≥ωΉή‘λΦέ”κΠ»ΒΡΙΊœΒΘ§≤ΔΖ÷ΈωΚ· ΐΕ®“ε”ρΘΜ
Θ®2Θ©άϊ”ΟΒΦ ΐ«σΚ· ΐΒΡΉν–Γ÷ΒΘ§Φ¥Ω…ΒΟΒΫΫα¬έ.
Θ®1Θ©ΙΐΒψFΉς![]() ”ΎΒψHΘ§‘ρ
”ΎΒψHΘ§‘ρ![]() Θ§
Θ§
Υυ“‘‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ°
Θ°
…η![]() Θ§
Θ§
‘ρ”…Χβ“βΒΟ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
Υυ“‘![]() Θ§
Θ§
Ι ¬ΖΟφABΒΡ‘λΦέΈΣ![]() «ß‘ΣΘ§
«ß‘ΣΘ§
≤ύ±ΏCFΚΆDEΒΡ‘λΦέΈΣ![]() «ß‘ΣΘ°
«ß‘ΣΘ°
ΒΉ≤ΩEFΒΡ‘λΦέΈΣ![]() Θ§
Θ§
Υυ“‘![]() Θ§
Θ§
”÷“ρΈΣ![]() Θ§
Θ§
‘ρ![]() Θ§
Θ§
…η»ώΫ«![]() ¬ζΉψ
¬ζΉψ![]() Θ§‘ρ
Θ§‘ρ![]() Θ°
Θ°
“ρ¥ΥΘ§![]() Θ§
Θ§![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ°
Θ°
Θ®2Θ©”…Θ®1Θ©÷Σ![]()
…η![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ§
Θ§
‘ρ![]() Θ°
Θ°
Νν![]() Θ§‘ρ
Θ§‘ρ![]() Θ°
Θ°
“ρΈΣ![]() Θ°
Θ°
Υυ“‘![]() Θ§Ν–±μ»γœ¬ΘΚ
Θ§Ν–±μ»γœ¬ΘΚ
|
|
|
|
|
|
| Θ≠ | 0 | ΘΪ | ||
| 4 |
Υυ“‘Β±![]() ±Θ§
±Θ§![]() Θ§”–
Θ§”–![]() Θ°
Θ°
¥πΘΚΒ±![]() ΒΡ÷ΒΈΣ
ΒΡ÷ΒΈΣ![]() ±Θ§Ήή‘λΦέΉνΒΆΘ§ΈΣ
±Θ§Ήή‘λΦέΉνΒΆΘ§ΈΣ![]() «ß‘ΣΘ°
«ß‘ΣΘ°