题目内容
4.下列命题中正确的是①②.①若△ABC在平面α外,它的三条边所在的直线分别交平面α于P,Q,R,则P,Q,R三点共线;
②若三条直线a,b,c互相平行且分别交直线l于A,B,C三点,则这四条直线共面;
③空间中不共面的五个点一定能确定10个平面;
④若a不平行于平面α,且a?α,则α内的所有直线与a异面.
分析 根据公理3可判断①;根据公理1,2可判断②;举出反例四个点共面,但第5个点与其它四点不共面,可判断③;根据空间直线与直线位置关系的几何特征,可判断④.
解答 解:①若△ABC在平面α外,它的三条边所在的直线分别交平面α于P,Q,R,
则P,Q,R均在平面ABC与平面α的交线上,
由公理3可得:P,Q,R三点共线,故①正确;
若三条直线a,b,c互相平行且分别交直线l于A,B,C三点,有公理2和公理1可得,则这四条直线共面,故②正确;
空间中不共面的五个点,当四个点共面,但第5个点与其它四点不共面时,只能确定1+${C}_{4}^{2}$=7个平面,故③错误;
若a不平行于平面α,且a?α则a∩α=A,则α内的所有不过交点A直线与a异面,过交点A的直线与a相交,故④错误;
故正确的命题为:①②,
故答案为:①②
点评 本题考查的知识点是命题的真假判断与应用,此类题型往往综合较多的其它知识点,综合性强,难度中档.

练习册系列答案
相关题目
19.已知命题p:?x0∈R,${9}^{{x}_{0}}$-m•${3}^{{x}_{0}}$+4≤0,若p为真命题,则实数m的取值范围是( )
| A. | (4,+∞) | B. | [4,+∞) | C. | (-∞,4) | D. | (-∞,4] |
9.(普通中学做)如图所示,程序框图输出的某一实数对(x,y)中,若y=32,则x=( )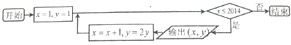
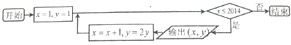
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |