题目内容
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区![]() 名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
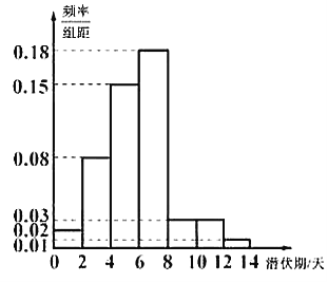
(1)求这![]() 名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这
名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这![]() 名患者中“长潜伏者”的人数;
名患者中“长潜伏者”的人数;
(2)现有![]() 名患者自愿报名某临床试验,其中“短潜伏者”
名患者自愿报名某临床试验,其中“短潜伏者”![]() 人,“长潜伏者”
人,“长潜伏者”![]() 人,医生从
人,医生从![]() 人中随机抽取两人做临床试验,求两人中恰有
人中随机抽取两人做临床试验,求两人中恰有![]() 人为“长潜伏者”的概率.
人为“长潜伏者”的概率.
【答案】(1)平均数为![]() ,这
,这![]() 名患者中“长潜伏者”的人数为
名患者中“长潜伏者”的人数为![]() 人;(2)
人;(2)![]() .
.
【解析】
(1)由频率分布直方图各段中间值乘以各段的概率再相加即为平均值,由频率分布直方图可知“长潜伏者”即潜伏期时间不低于![]() 天的频率,将其乘以样本总量即可;
天的频率,将其乘以样本总量即可;
(2)由分层抽样知![]() 人中,“短潜伏者”有
人中,“短潜伏者”有![]() 人,记为
人,记为![]() 、
、![]() 、
、![]() ,“长潜伏者”有
,“长潜伏者”有![]() 人,记为
人,记为![]() 、
、![]() 、
、![]() 、
、![]() ,列出所有基本事件可能,再由古典概型概率计算公式求解.
,列出所有基本事件可能,再由古典概型概率计算公式求解.
(1)平均数![]() .
.
由频率分布直方图可知“长潜伏者”即潜伏期时间不低于![]() 天的频率为
天的频率为![]() ,
,
所以500人中“长潜伏者”的人数为![]() 人;
人;
(2)由分层抽样知![]() 人中,“短潜伏者”有
人中,“短潜伏者”有![]() 人,记为
人,记为![]() 、
、![]() 、
、![]() ,“长潜伏者”有
,“长潜伏者”有![]() 人,记为
人,记为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
从中抽取![]() 人,共有
人,共有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共有
,共有![]() 种不同的结果,
种不同的结果,
两人中恰好有![]() 人为“长潜伏者”包含了
人为“长潜伏者”包含了![]() 种结果.
种结果.
所以所求概率![]()

 名校课堂系列答案
名校课堂系列答案【题目】2020年初,由于疫情影响,开学延迟,为了不影响学生的学习,国务院、省市区教育行政部门倡导各校开展“停学不停课、停学不停教”,某校语文学科安排学生学习内容包含老师推送文本资料学习和视频资料学习两类,且这两类学习互不影响已知其积分规则如下:每阅读一篇文本资料积1分,每日上限积5分;观看视频1个积2分,每日上限积6分.经过抽样统计发现,文本资料学习积分的概率分布表如表1所示,视频资料学习积分的概率分布表如表2所示.
表1
文本学习积分 | 1 | 2 | 3 | 4 | 5 |
概率 |
|
|
|
|
|
表2
视频学习积分 | 2 | 4 | 6 |
概率 |
|
|
|
(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.