Question

【题目】已知如图所示的三棱锥D﹣ABC的四个顶点均在球O的球面上，△ABC和△DBC所在平面相互垂直，AB=3，AC=，BC=CD=BD=2，则球O的表面积为（ ）

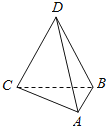
A．4π B．12π C．16π D．36π

Answer 1

【答案】C

【解析】

试题证明AC⊥AB，可得△ABC的外接圆的半径为，利用△ABC和△DBC所在平面相互垂直，球心在BC边的高上，设球心到平面ABC的距离为h，则h2+3=R2=（﹣h）2，求出球的半径，即可求出球O的表面积．

解：∵AB=3，AC=，BC=2，

∴AB2+AC2=BC2，

∴AC⊥AB，

∴△ABC的外接圆的半径为，

∵△ABC和△DBC所在平面相互垂直，

∴球心在BC边的高上，

设球心到平面ABC的距离为h，则h2+3=R2=（﹣h）2，

∴h=1，R=2，

∴球O的表面积为4πR2=16π．

故选：C．