Question

【题目】已知函数f（x）＝x2+ax+blnx（a，b∈R），曲线y＝f（x）在点（1，f（1））处的切线方程为2x﹣y﹣2＝0．

（1）判断f（x）在定义域内的单调性，并说明理由；

（2）若对任意的x∈（1，+∞），不等式f（x）≤m（ex﹣1﹣1）恒成立，求实数m的取值范围．

Answer 1

【答案】（1）f（x）在（0，+∞）上为增函数；见解析（2）[2，+∞）

【解析】

求出原函数的导函数，利用f′(1)＝2及f(1)＝0联立不等式组求解a，b的值，则函数解析式可求．(1)由f′(x)＞0在(0，+∞)上恒成立，可得f(x)在(0，+∞)上为增函数；

(2)对任意的x∈(1，+∞)，不等式f(x)≤m(ex﹣1﹣1)恒成立，即x2﹣x+lnx≤m(ex﹣1﹣1)恒成立，令g(x)＝m(ex﹣1﹣1)﹣x2+x﹣lnx，求其导函数，分析可知当m≥2时，g′(x)＞g′(1)≥0，g(x)单调递增，则g(x)＞g(1)＝0；当0＜m＜2时，g′(x)＝0在(1，+∞)上必有实数根，设最小的正数根为x0，当x∈(1，x0)时，g′(x)＜0，g(x)单调递减，则g(x)＜g(1)＝0，与题设不符；当m≤0时，g′(x)＜0，则g(x)单调递减，g(x)＜g(1)＝0，与题意不符．

解：由f(x)＝x2+ax+blnx，得f′(x)＝2x+a(x＞0)．

由曲线y＝f(x)在点(1，f(1))处的切线方程为2x﹣y﹣2＝0，

得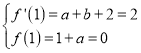，即a＝﹣1，b＝1．

∴f(x)＝x2﹣x+lnx．

(1)∵f′(x)＝2x﹣1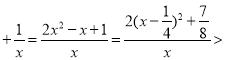0在(0，+∞)上恒成立，

∴f(x)在(0，+∞)上为增函数；

(2)由(1)得，f(x)＝x2﹣x+lnx，

对任意的x∈(1，+∞)，不等式f(x)≤m(ex﹣1﹣1)恒成立，

即x2﹣x+lnx≤m(ex﹣1﹣1)恒成立，

令g(x)＝m(ex﹣1﹣1)﹣f(x)＝m(ex﹣1﹣1)﹣x2+x﹣lnx，

则g′(x)，注意到g(1)＝0，g′(1)＝m﹣2，

要使得对任意的x∈(1，+∞)，不等式f(x)≤m(ex﹣1﹣1)恒成立，即g(x)≥0，

则必有g′(x)在(1，1+δ)(其中δ为任意小的正数)大于0，亦有g′(1)≥0，则m≥2．

当m≥2时，令u(x)＝g′(x)，

u′(x)2ex﹣1﹣2＞0．

∴u(x)在(1，+∞)上单调递增，则g′(x)＞g′(1)≥0，

∴g(x)单调递增，则g(x)＞g(1)＝0；

当0＜m＜2时，g′(1)＝m﹣2＜0，当x→+∞时，g′(x)→+∞，

则g′(x)＝0在(1，+∞)上必有实数根，设最小的正数根为x0，

则当x∈(1，x0)时，g′(x)＜0，g(x)单调递减，则g(x)＜g(1)＝0，与题设不符；

当m≤0时，g′(x)0，则g(x)单调递减，g(x)＜g(1)＝0，与题意不符．

综上所述，m的取值范围为[2，+∞)．