题目内容
(本题满分12分)已知函数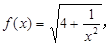 数列
数列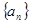 的前n项和为
的前n项和为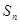 ,
,
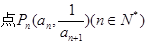 ,在曲线
,在曲线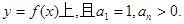
(1)求数列{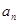 }的通项公式
}的通项公式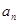 ;(II)数列{
;(II)数列{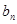 }首项b1=1,前n项和Tn,且
}首项b1=1,前n项和Tn,且
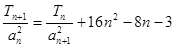 ,求数列{
,求数列{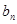 }通项公式bn.
}通项公式bn.
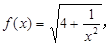 数列
数列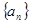 的前n项和为
的前n项和为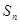 ,
,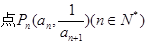 ,在曲线
,在曲线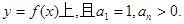
(1)求数列{
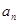 }的通项公式
}的通项公式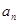 ;(II)数列{
;(II)数列{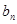 }首项b1=1,前n项和Tn,且
}首项b1=1,前n项和Tn,且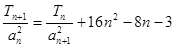 ,求数列{
,求数列{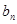 }通项公式bn.
}通项公式bn.(I)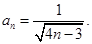 (II)
(II)
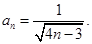 (II)
(II)
试题分析:(1)
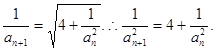
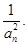 是等差数列,,进而整体的思想得到数列。
是等差数列,,进而整体的思想得到数列。(2) 由题设知

 这是这一问的一个难点也是突破口。
这是这一问的一个难点也是突破口。解:(I)由题意知
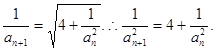
 是等差数列.…………………………………2分
是等差数列.…………………………………2分
 ………………………………6分
………………………………6分(II)由题设知


 是等差数列.…………………………………8分
是等差数列.…………………………………8分
 ……………………10分
……………………10分∴当n=1时,
 ;
;当

经验证n=1时也适合上式.
 …………………………12分
…………………………12分点评:解决该试题的关键是利用整体的思想来求解数列的通项公式,以及数列的定义整体来证明
 是等差数列,从而得到Tn的值。
是等差数列,从而得到Tn的值。
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
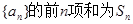 ,
,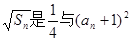 的等比中项。
的等比中项。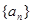 是等差数列;(2)若
是等差数列;(2)若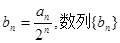 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。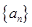 的首项为
的首项为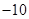 、公差为2,则它的前n项
、公差为2,则它的前n项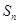 的最小值是______________。
的最小值是______________。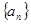 满足
满足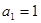 ,且对任意的
,且对任意的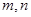
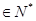 都有:
都有: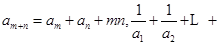
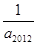 等于 ( )
等于 ( )


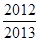
 的前10项中,所有偶数项、所有奇数项之和分别为55和45,则它的首项
的前10项中,所有偶数项、所有奇数项之和分别为55和45,则它的首项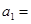 _______。
_______。 ,
, 则它的公差是( )
则它的公差是( )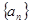 的通项为
的通项为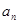 =
=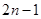 ,
,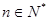 ,其前
,其前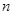 项和为
项和为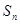 ,则使
,则使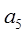 =10,且
=10,且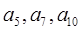 是等比数列{
是等比数列{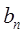 }的第1,3,5项,且
}的第1,3,5项,且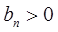 .
.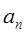 }的第20项,(2)求数列{
}的第20项,(2)求数列{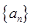 中,
中, ,
, ,当
,当 时,序号
时,序号 等于( )
等于( )