题目内容
10.4个不同的球放入编号为1,2,3,4的四个盒子中,每个盒子中球的个数不大于盒子的编号,则共有175种方法(用数字作答)分析 根据题意,分4种情况讨论:(1)四个盒子都放,(2)4个球放到三个盒子里,(3)4个球放到两个盒子里,(4)4个球放一个盒子,分别求出每种情况下的放法数目,由分类计数原理计算可得答案.
解答 解:根据题意,分4种情况讨论:
(1)四个盒子都放,每个盒子里都放1个球,将4个球全排列即可:有$A_4^4=24$种情况,
(2)4个球放到三个盒子里,有$C_4^2C_3^1A_3^2=108$种情况,
(3)4个球放到两个盒子里,有$\frac{C_4^2}{A_2^2}A_3^2$+$C_4^3C_2^1C_3^1$=42种情况,
(4)4个球放一个盒子,只能放在编号为4的盒子里,有1种情况,
所以共有24+108+42+1=175种放法;
故答案为:175.
点评 本题考查排列组合的运用,涉及分类计数原理的应用,注意分类讨论是做到不重不漏.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
1.设(x-$\frac{2}{\sqrt{x}}$)6的展开式中的常数为M,所有二项式系数和为N,则M+N=( )
| A. | 304 | B. | -304 | C. | 136 | D. | -136 |
5.与命题“若p则q”的否命题必定同真假的命题为( )
| A. | 若q则p | B. | 若p则q | C. | 若¬q则p | D. | 若¬q则¬p |
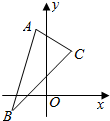 已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).
已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).