题目内容
等边三角形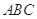 的边长为3,点
的边长为3,点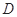 、
、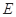 分别是边
分别是边 、
、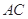 上的点,且满足
上的点,且满足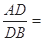
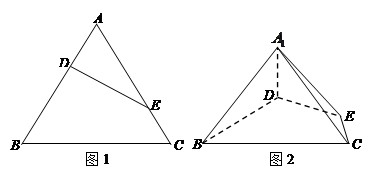
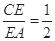 (如图1).将△
(如图1).将△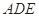 沿
沿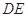 折起到△
折起到△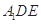 的位置,使二面角
的位置,使二面角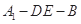 成直二面角,连结
成直二面角,连结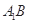 、
、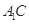 (如图2).
(如图2).
(1)求证: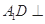 平面
平面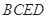 ;
;
(2)在线段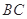 上是否存在点
上是否存在点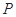 ,使直线
,使直线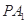 与平面
与平面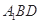 所成的角为
所成的角为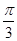 ?若存在,求出
?若存在,求出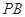 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
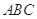 的边长为3,点
的边长为3,点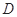 、
、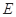 分别是边
分别是边 、
、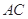 上的点,且满足
上的点,且满足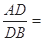
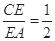 (如图1).将△
(如图1).将△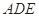 沿
沿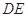 折起到△
折起到△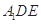 的位置,使二面角
的位置,使二面角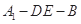 成直二面角,连结
成直二面角,连结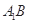 、
、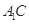 (如图2).
(如图2).(1)求证:
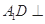 平面
平面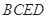 ;
;(2)在线段
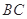 上是否存在点
上是否存在点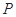 ,使直线
,使直线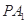 与平面
与平面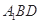 所成的角为
所成的角为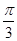 ?若存在,求出
?若存在,求出 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
(1)参考解析; (2)

试题分析:(1) 由
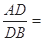
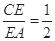 ,等边三角形
,等边三角形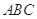 的边长为3.所以可得
的边长为3.所以可得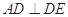 ,所以在三角形ADE翻折过程中
,所以在三角形ADE翻折过程中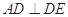 始终成立.又由于
始终成立.又由于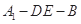 成直二面角.由平面与平面垂直的性质定理可得
成直二面角.由平面与平面垂直的性质定理可得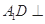 平面
平面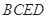 .
.(2)由于平面
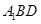
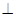 平面BCED.假设存在点P,过点P作BD的垂线,垂足为H.则
平面BCED.假设存在点P,过点P作BD的垂线,垂足为H.则 为所求的角.假设BP的长为x,根据题意分别求出相应的线段
为所求的角.假设BP的长为x,根据题意分别求出相应的线段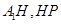 .即可得结论.
.即可得结论.(1) 因为等边△
 的边长为3,且
的边长为3,且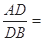
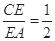 ,
, 所以
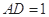 ,
,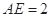 .
.在△
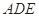 中,
中,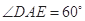 ,
, 由余弦定理得
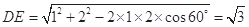 .
.因为
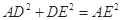 ,
, 所以
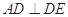 . (4分)
. (4分)折叠后有

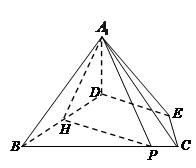
因为二面角
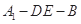 是直二面角,所以平面
是直二面角,所以平面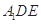
 平面
平面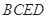
又平面
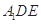
 平面
平面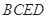
 ,
,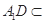 平面
平面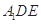 ,
, ,
, 所以
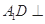 平面
平面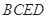 (6分)
(6分)(2)由(1)的证明,可知
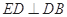 ,
,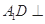 平面
平面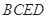 .
.以
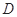 为坐标原点,以射线
为坐标原点,以射线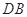 、
、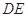 、
、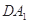 分别为
分别为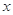 轴、
轴、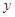 轴、
轴、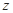 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系 如图
如图
设
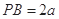
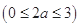 ,
, 则
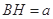 ,
,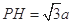 ,
,
所以
 ,
,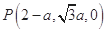 ,
,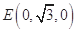
所以
 (8分)
(8分)因为
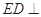 平面
平面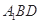 ,
, 所以平面
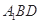 的一个法向量为
的一个法向量为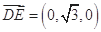
因为直线
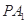 与平面
与平面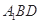 所成的角为
所成的角为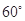 ,
, 所以
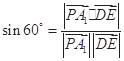
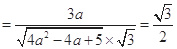 , (10分)
, (10分)解得
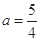
即
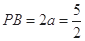 ,满足
,满足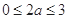 ,符合题意
,符合题意 所以在线段
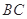 上存在点
上存在点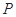 ,使直线
,使直线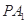 与平面
与平面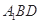 所成的角为
所成的角为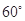 ,此时
,此时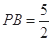 (12分)
(12分)
练习册系列答案
相关题目
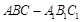 中,侧面
中,侧面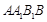 为菱形,且
为菱形,且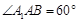 ,
,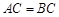 ,
,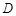 是
是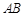 的中点.
的中点.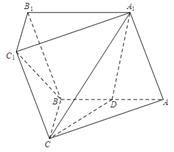
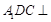 平面
平面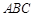 ;
;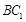 ∥平面
∥平面 .
.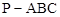 中,已知
中,已知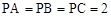 ,
,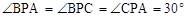 , 一绳子从A点绕三棱锥侧面一圈回到点A的距离中,绳子最短距离是_____________.
, 一绳子从A点绕三棱锥侧面一圈回到点A的距离中,绳子最短距离是_____________.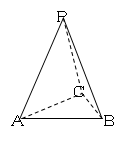
 分别是正方体
分别是正方体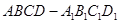 的棱
的棱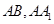 的中点,点
的中点,点 分别是线段
分别是线段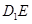 与
与 上的点,则满足与平面
上的点,则满足与平面 平行的直线
平行的直线 有( )
有( )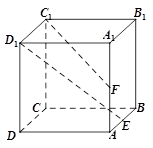
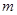 ,
,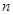 是空间中两条不同的直线,
是空间中两条不同的直线,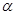 ,
, ,
,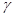 是空间中三个不同的平面,则
是空间中三个不同的平面,则 下列命题正确的序号是 .
下列命题正确的序号是 .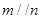 ,
,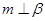 ,则
,则 ; ②若
; ②若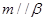 ,则
,则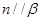 ;
;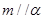 ,
, ; ④若
; ④若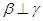 ,则
,则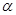 、
、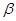 是两个不同的平面,则
是两个不同的平面,则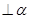 ,则n
,则n
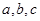 表示不同直线,M表示平面,给出四个命题:①若
表示不同直线,M表示平面,给出四个命题:①若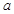 ∥M,
∥M,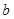 ∥M,则
∥M,则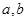 相交或
相交或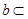 M,
M,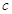 ,
,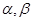 和直线
和直线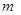 ,给出条件:①
,给出条件:① ;②
;②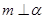 ;③
;③ ;④
;④ ;⑤
;⑤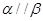 .为使
.为使 ,应选择下面四个选项中的( )
,应选择下面四个选项中的( )