题目内容
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.
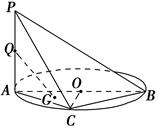
(1)求证:BC⊥平面PAC;
(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.

(1)求证:BC⊥平面PAC;
(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
见解析
(1)由AB是圆O的直径,得AC⊥BC,
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以BC⊥平面PAC.
(2)连接OG并延长交AC于M,连接QM,QO,由G为△AOC的重心,得M为AC中点.
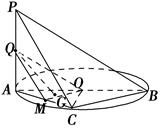
由Q为PA中点,得QM∥PC,
又O为AB中点,得OM∥BC.
因为QM∩MO=M,QM?平面QMO,
MO?平面QMO,BC∩PC=C,
BC?平面PBC,PC?平面PBC.
所以平面QMO∥平面PBC.
因为QG?平面QMO,所以QG∥平面PBC.
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以BC⊥平面PAC.
(2)连接OG并延长交AC于M,连接QM,QO,由G为△AOC的重心,得M为AC中点.

由Q为PA中点,得QM∥PC,
又O为AB中点,得OM∥BC.
因为QM∩MO=M,QM?平面QMO,
MO?平面QMO,BC∩PC=C,
BC?平面PBC,PC?平面PBC.
所以平面QMO∥平面PBC.
因为QG?平面QMO,所以QG∥平面PBC.

练习册系列答案
相关题目
 中,点
中,点 为边
为边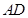 上的点,点
上的点,点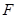 为边
为边 的中点,
的中点,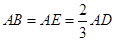 ,现将
,现将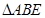 沿
沿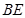 边折至
边折至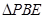 位置,且平面
位置,且平面 平面
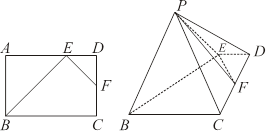
平面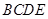 .
.
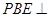 平面
平面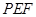 ;
;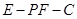 的大小.
的大小.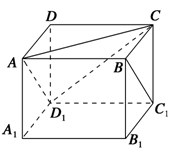
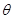 ,那么
,那么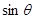 为 .
为 .