Question

【题目】如图，设椭圆C： （a＞b＞0），动直线l与椭圆C只有一个公共点P，且点P在第一象限．
（Ⅰ）已知直线l的斜率为k，用a，b，k表示点P的坐标；
（Ⅱ）若过原点O的直线l1与l垂直，证明：点P到直线l1的距离的最大值为a﹣b．

Answer 1

【答案】解：（Ⅰ）设直线l的方程为y=kx+m（k＜0），由 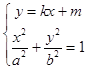，消去y得
（b2+a2k2）x2+2a2kmx+a2m2﹣a2b2=0．
由于直线l与椭圆C只有一个公共点P，故△=0，即b2﹣m2+a2k2=0，
此时点P的横坐标为﹣ ，代入y=kx+m得
点P的纵坐标为﹣k +m= ，
∴点P的坐标为（﹣ ， ），
又点P在第一象限，故m＞0，
故m= ，
故点P的坐标为P（ ， ）．
（Ⅱ）由于直线l1过原点O且与直线l垂直，故直线l1的方程为x+ky=0，所以点P到直线l1的距离
d= ，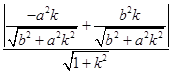
整理得：d= ，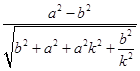
因为a2k2+ ≥2ab，所以 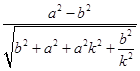≤ =a﹣b，当且仅当k2= 时等号成立．
所以，点P到直线l1的距离的最大值为a﹣b．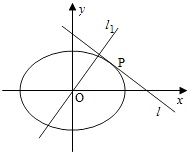

【解析】（Ⅰ）设直线l的方程为y=kx+m（k＜0），由 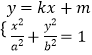，消去y得（b2+a2k2）x2+2a2kmx+a2m2﹣a2b2=0，利用△=0，可求得在第一象限中点P的坐标；（Ⅱ）由于直线l1过原点O且与直线l垂直，设直线l1的方程为x+ky=0，利用点到直线间的距离公式，可求得点P到直线l1的距离d= 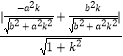，整理即可证得点P到直线l1的距离的最大值为a﹣b．．