题目内容
【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为![]() ,点(0,
,点(0,![]() )是椭圆与y轴的一个交点.
)是椭圆与y轴的一个交点.
(1)求椭圆C的方程;
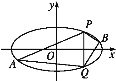
(2)直线x=2与椭圆交于P,Q两点,点P位于第一象限,A,B是椭圆上位于直线x=2两侧的动点;
①若直线AB的斜率为![]() ,求四边形APBQ面积的取值范围;
,求四边形APBQ面积的取值范围;
②当点A,B在椭圆上运动,且满足∠APQ=∠BPQ时,直线AB的斜率是否为定值?若是,求出此定值;若不是,说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
⑴设椭圆的方程为![]() =1(a>b>0),由椭圆的性质求出
=1(a>b>0),由椭圆的性质求出![]() ,由此求得椭圆
,由此求得椭圆![]() 的方程
的方程
⑵①设A(x1,y1),B(x2,y2),直线AB的方程为![]() ,与椭圆联立,得到
,与椭圆联立,得到![]() ,由此利用韦达定理,弦长公式求出四边形APBQ的面积的取值范围
,由此利用韦达定理,弦长公式求出四边形APBQ的面积的取值范围
②当![]() 时,设直线PA的方程为
时,设直线PA的方程为![]() ,分别与椭圆方程联立,利用韦达定理即可求得答案
,分别与椭圆方程联立,利用韦达定理即可求得答案
(1)设椭圆的方程为![]() =1(a>b>0),由题意可知,b=
=1(a>b>0),由题意可知,b=![]() ,a2=b2+c2,解得a=2
,a2=b2+c2,解得a=2![]() ,
,
∴椭圆C的方程为![]() =1.
=1.
(2)①设A(x1,y1),B(x2,y2),直线AB的方程为y=![]() x+t,
x+t,
联立
消y可得,2x2+4tx+4t2-8=0,
即x2+2tx+2t2-4=0,
则有x1+x2=-2t,x1x2=2t2-4.
对于![]() =1,令x=2,得P(2,1),Q(2,-1),
=1,令x=2,得P(2,1),Q(2,-1),
将P,Q分别代入直线可得,t=0,t=-2,
由点A,B在直线x=2的两侧,故-2<t<0,
四边形APBQ的面积为
S=S△APQ+S△BPQ
=![]() |PQ|·|x2-x1|
|PQ|·|x2-x1|
=![]() ×2×|x2-x1|
×2×|x2-x1|
=![]()
=![]() ,
,
而-2<t<0,所以0<S四边形APBQ<4.
②当∠APQ=∠BPQ时,直线PA,PB的斜率之和为0,
不妨设直线PA的斜率为k,则直线PB的斜率为-k,
所以直线PA的方程为y-1=k(x-2),
即kx-y+1-2k=0,
联立
消去y可得,(1+4k2)x2+8k(1-2k)x+4(1-2k)2-8=0,
所以x1+2=![]() .
.
同理直线PB的方程为y-1=-k(x-2),
可得,x2+2=![]() ,
,
所以x1+x2=![]() ,x1-x2=
,x1-x2=![]() ,
,
所以kAB=![]()
=![]()
=![]()
=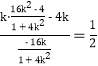 ,
,
故直线AB的斜率为定值![]() .
.


