题目内容
如图,在四棱锥PABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,DC∥AB,∠BAD=90°,且AB=2AD=2DC=2PD=4,E为PA的中点.
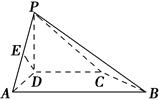
(1)求证:DE∥平面PBC;
(2)求证:DE⊥平面PAB.

(1)求证:DE∥平面PBC;
(2)求证:DE⊥平面PAB.
(1)见解析(2)见解析
(1)设PB的中点为F,连接EF、CF,EF∥AB,DC∥AB,

所以EF∥DC,且EF=DC=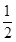 AB.
AB.
故四边形CDEF为平行四边形,可得ED∥CF.
又ED?平面PBC,CF?平面PBC,
故DE∥平面PBC.
(2)因为PD⊥底面ABCD,AB?平面ABCD,
所以AB⊥PD.
又因为AB⊥AD,PD∩AD=D,AD?平面PAD,PD?平面PAD,所以AB⊥平面PAD.
ED?平面PAD,故ED⊥AB.又PD=AD,E为PA的中点,故ED⊥PA;
PA∩AB=A,PA?平面PAB,AB?平面PAB,
所以ED⊥平面PAB.

所以EF∥DC,且EF=DC=
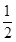 AB.
AB.故四边形CDEF为平行四边形,可得ED∥CF.
又ED?平面PBC,CF?平面PBC,
故DE∥平面PBC.
(2)因为PD⊥底面ABCD,AB?平面ABCD,
所以AB⊥PD.
又因为AB⊥AD,PD∩AD=D,AD?平面PAD,PD?平面PAD,所以AB⊥平面PAD.
ED?平面PAD,故ED⊥AB.又PD=AD,E为PA的中点,故ED⊥PA;
PA∩AB=A,PA?平面PAB,AB?平面PAB,
所以ED⊥平面PAB.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
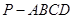 中,底面
中,底面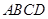 是平行四边形,
是平行四边形,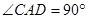 ,
,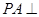 平面
平面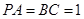 ,
,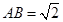 ,
,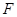 是
是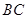 的中点.
的中点.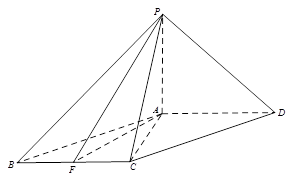
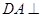 平面
平面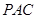 ;
; 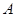 为坐标原点,射线
为坐标原点,射线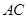 、
、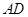 、
、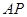 分别是
分别是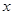 轴、
轴、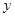 轴、
轴、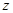 轴的正半轴,建立空间直角坐标系,已经计算得
轴的正半轴,建立空间直角坐标系,已经计算得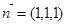 是平面
是平面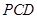 的法向量,求平面
的法向量,求平面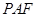 与平面
与平面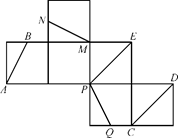
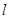 不平行于平面
不平行于平面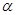 ,且
,且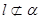 ,则( )
,则( )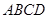 中,
中,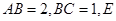 为
为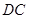 的中点,
的中点,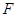 为线段
为线段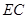 (端点除外)上一动点,现将
(端点除外)上一动点,现将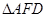 沿
沿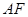 折起,使平面
折起,使平面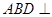 平面
平面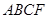 .在平面
.在平面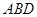 内过点
内过点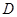 作
作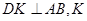 为垂足,设
为垂足,设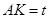 ,则
,则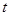 的取值范围是________
的取值范围是________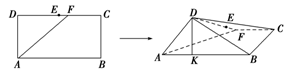

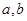 以及平面
以及平面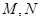 ,下列命题中正确的是 ( )
,下列命题中正确的是 ( )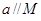 ,
,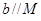 ,则
,则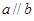
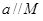 ,
,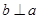 ,则
,则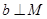
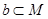 ,且
,且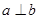 ,则
,则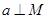
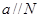 ,则
,则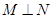
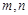 是两条不重合的直线,
是两条不重合的直线,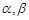 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: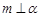 ,
,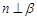 ,且
,且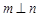 ,则
,则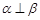 ;
;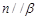 ,且
,且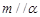 ,
,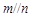 ,则
,则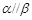 ;
;