题目内容
如图,在长方形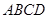 中,
中,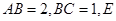 为
为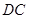 的中点,
的中点,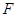 为线段
为线段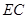 (端点除外)上一动点,现将
(端点除外)上一动点,现将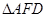 沿
沿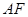 折起,使平面
折起,使平面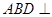 平面
平面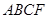 .在平面
.在平面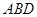 内过点
内过点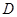 作
作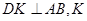 为垂足,设
为垂足,设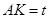 ,则
,则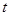 的取值范围是________
的取值范围是________
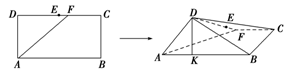
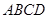 中,
中,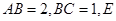 为
为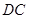 的中点,
的中点,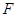 为线段
为线段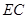 (端点除外)上一动点,现将
(端点除外)上一动点,现将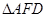 沿
沿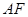 折起,使平面
折起,使平面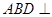 平面
平面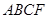 .在平面
.在平面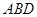 内过点
内过点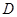 作
作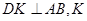 为垂足,设
为垂足,设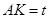 ,则
,则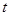 的取值范围是________
的取值范围是________
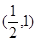
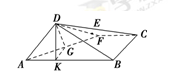
试题分析:分析:如图,过
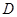 作
作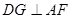 ,垂足为
,垂足为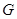 ,连接
,连接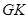 ,
,
∵平面
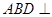 平面
平面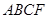 ,
, ,
,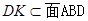 ,
, ,
,∴
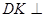 平面
平面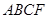 ,
, ,∴
,∴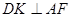 .因为
.因为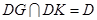 ,∴
,∴ 平面
平面 ,
,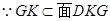 ∴
∴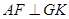 .
.容易得到,当
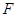 接近
接近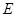 点时,
点时,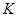 接近
接近 的中点,当
的中点,当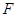 接近
接近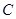 点时,
点时,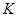 接近
接近 的四等分点,
的四等分点,∴t的取值范围是
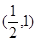 .
.
练习册系列答案
相关题目
 底面ABCD,
底面ABCD,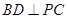 ,E是PA的中点.
,E是PA的中点.
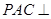 平面EBD;
平面EBD;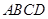 中,
中, 分别是
分别是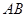 和
和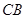 上的点,
上的点,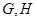 分别是
分别是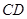 和
和 上的点,且
上的点,且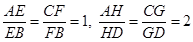 ,求证:
,求证: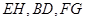 三条直线相交于同一点.
三条直线相交于同一点.
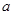 的正方体
的正方体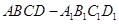 中,点
中,点 是棱
是棱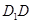 的中点,点
的中点,点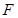 在棱
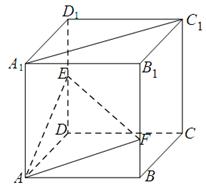
在棱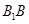 上,且满足
上,且满足 .
.
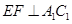 ;
;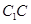 上确定一点
上确定一点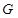 ,使
,使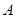 、
、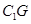 的长;
的长; 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.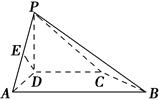
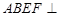 平面
平面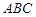 ,四边形
,四边形 为矩形,△
为矩形,△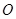 为
为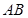 的中点,
的中点,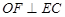 .
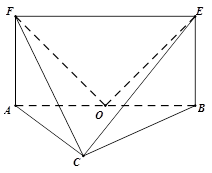
.
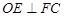 ;
; 的正切值.
的正切值.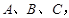 且
且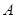 ={直线},
={直线},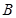 ={平面},
={平面},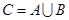 ,若
,若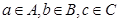 ,有四个命题①
,有四个命题①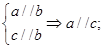 ②
②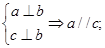 ③
③ ④
④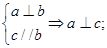 其中所有正确命题的序号是( )
其中所有正确命题的序号是( )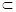 α,m
α,m