题目内容
已知函数f(x)=
x3-
x2+bx+a(a,b∈R),且其导函数f′(x)的图象过原点.
(Ⅰ)当a=1时,求函数f(x)的图象在x=3处的切线方程;
(Ⅱ)若存在x<0,使得f′(x)=-9,求a的最大值;
(Ⅲ)当a>0时,求函数f(x)的零点个数.
| 1 |
| 3 |
| a+1 |
| 2 |
(Ⅰ)当a=1时,求函数f(x)的图象在x=3处的切线方程;
(Ⅱ)若存在x<0,使得f′(x)=-9,求a的最大值;
(Ⅲ)当a>0时,求函数f(x)的零点个数.
f(x)=
x3-
x2+bx+a,f'(x)=x2-(a+1)x+b
由f'(0)=0得b=0,f'(x)=x(x-a-1).
(Ⅰ)当a=1时,f(x)=
x3-x2+1,f'(x)=x(x-2),f(3)=1,f'(3)=3
所以函数f(x)的图象在x=3处的切线方程为y-1=3(x-3),即3x-y-8=0;
(Ⅱ)存在x<0,使得f'(x)=x(x-a-1)=-9,-a-1=-x-
=(-x)+(-
)≥2
)=6,a≤-7,
当且仅当x=-3时,a=-7,所以a的最大值为-7;
(Ⅲ)当a>0时,x,f'(x),f(x)的变化情况如下表:
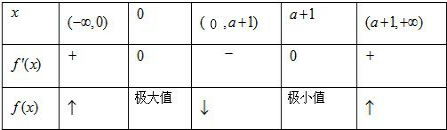
f(x)的极大值f(0)=a>0,
f(x)的极小值f(a+1)=a-
(a+1)3=-
[a3+3(a-
)2+
]<0
又f(-2)=-a-
<0,f(x)=
x2[x-
(a+1)]+a,f(
(a+1))=a>0.
所以函数f(x)在区间(-2,0),(0,a+1),(a+1,
(a+1))内各有一个零点,
故函数f(x)共有三个零点.
| 1 |
| 3 |
| a+1 |
| 2 |
由f'(0)=0得b=0,f'(x)=x(x-a-1).
(Ⅰ)当a=1时,f(x)=
| 1 |
| 3 |
所以函数f(x)的图象在x=3处的切线方程为y-1=3(x-3),即3x-y-8=0;
(Ⅱ)存在x<0,使得f'(x)=x(x-a-1)=-9,-a-1=-x-
| 9 |
| x |
| 9 |
| x |
(-x)•(-
|
当且仅当x=-3时,a=-7,所以a的最大值为-7;
(Ⅲ)当a>0时,x,f'(x),f(x)的变化情况如下表:

f(x)的极大值f(0)=a>0,
f(x)的极小值f(a+1)=a-
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 4 |
又f(-2)=-a-
| 14 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
所以函数f(x)在区间(-2,0),(0,a+1),(a+1,
| 3 |
| 2 |
故函数f(x)共有三个零点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
