题目内容
已知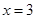 是函数
是函数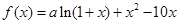 的一个极值点。
的一个极值点。
(Ⅰ)求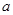 ;
;
(Ⅱ)求函数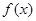 的单调区间;
的单调区间;
(Ⅲ)若直线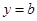 与函数
与函数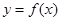 的图象有3个交点,求
的图象有3个交点,求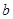 的取值范围。
的取值范围。
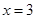 是函数
是函数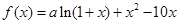 的一个极值点。
的一个极值点。(Ⅰ)求
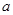 ;
;(Ⅱ)求函数
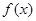 的单调区间;
的单调区间;(Ⅲ)若直线
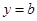 与函数
与函数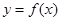 的图象有3个交点,求
的图象有3个交点,求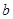 的取值范围。
的取值范围。(Ⅰ)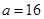 ;(Ⅱ)单调增区间是
;(Ⅱ)单调增区间是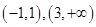 ,单调减区间是
,单调减区间是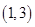 ;
;
(Ⅲ)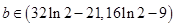
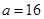 ;(Ⅱ)单调增区间是
;(Ⅱ)单调增区间是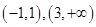 ,单调减区间是
,单调减区间是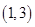 ;
;(Ⅲ)
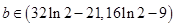
试题分析:(Ⅰ)因为
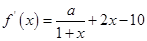 ,
,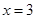 是函数
是函数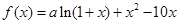 的一个极值点,所以
的一个极值点,所以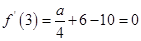 ,
,因此
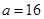 . ---3分
. ---3分(Ⅱ)由(Ⅰ)知,
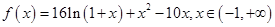
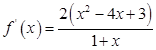 ,
,当
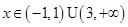 时,
时,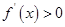
当
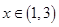 时,
时,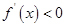
所以
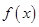 的单调增区间是
的单调增区间是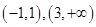 , ---6分
, ---6分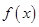 的单调减区间是
的单调减区间是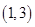 . ---8分
. ---8分(Ⅲ)由(Ⅱ)知,
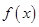 在
在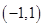 内单调增加,在
内单调增加,在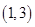 内单调减少,在
内单调减少,在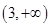 上单调增加,
上单调增加,且当
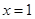 或
或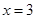 时,
时,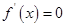
所以
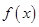 的极大值为
的极大值为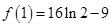 ,极小值为
,极小值为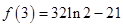 . ---10分
. ---10分因此
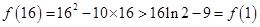
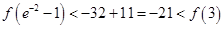
所以在
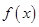 的三个单调区间
的三个单调区间 ,
,因为直线
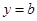 有
有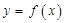 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当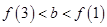
因此,
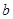 的取值范围为
的取值范围为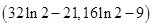 . ---12分
. ---12分点评:导数的工具性使得导数在高考中的应用有得天独厚的优势,特别是在研究函数的性质方面.近年,各地高考都从不同的方面对导数内容进行考查,既有考查导数的小题,又有考查导数综合应用的大题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
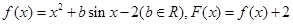 ,且对于任意实数
,且对于任意实数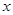 ,恒有
,恒有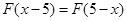 .
.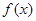 的解析式;
的解析式;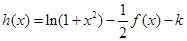 有几个零点?
有几个零点?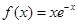 ,
,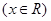 .
.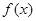 的单调区间和极值;
的单调区间和极值;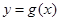 的图象与函数
的图象与函数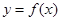 的图象关于直线
的图象关于直线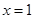 对称;
对称;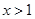 时,
时,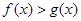
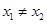 且
且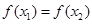 ,证明
,证明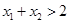
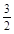 ,
,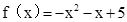
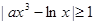 对任意
对任意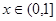 都成立,则实数a取值范围是 。
都成立,则实数a取值范围是 。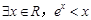 ”的否定是( )
”的否定是( )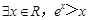
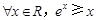
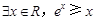
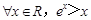
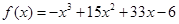 的单调增区间为 .
的单调增区间为 .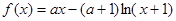 ..
..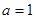 时,求
时,求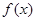 的单调区间;
的单调区间;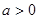 时,设
时,设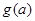 ,若
,若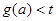 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.