题目内容
【题目】某地区2011年至2017年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求样本中心点坐标;
(2)已知两变量线性相关,求y关于t的线性回归方程;
(3)利用(2)中的线性回归方程,分析2011年至2017年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2019年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: .
.
【答案】(1)![]() ;(2)
;(2)![]() =0.5t+2.3;(3)见解析
=0.5t+2.3;(3)见解析
【解析】
(1)由表中数据计算![]() 、
、![]() 即可;
即可;
(2)由所给数据计算出回归系数,写出回归方程即可;
(3)由![]() =0.5>0知y关于t正相关,求出t=9时
=0.5>0知y关于t正相关,求出t=9时![]() 的值即可.
的值即可.
(1)由所给数据计算得
![]() (1+2+3+4+5+6+7)=4,
(1+2+3+4+5+6+7)=4,
![]() (2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
所以样本中心点为![]() .
.
(2)![]() =9+4+1+0+1+4+9=28,
=9+4+1+0+1+4+9=28,
![]() =(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,
=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,
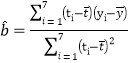 =
=![]() =0.5,
=0.5,![]() =4.3-0.5×4=2.3,
=4.3-0.5×4=2.3,
故所求线性回归方程为![]() =0.5t+2.3.
=0.5t+2.3.
(3)由(2)知,![]() =0.5>0,故2011年至2017年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.将2019年的年份代号t=9代入(2)中的线性回归方程,得
=0.5>0,故2011年至2017年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.将2019年的年份代号t=9代入(2)中的线性回归方程,得![]() =0.5×9+2.3=6.8,故预测该地区2019年农村居民家庭人均纯收入为6.8千元.
=0.5×9+2.3=6.8,故预测该地区2019年农村居民家庭人均纯收入为6.8千元.

【题目】我校高二年级共2000名学生,其中男生1200人.为调查学生们的手机使用情况,采用分层抽样的方法,随机抽取100位学生每周平均使用手机上网时间的样本数据(单位:小时).根据这100个数据,得到学生每周平均使用手机上网时间的频率分布直方图(如图所示),其中样本数据分组区间分别为![]() .
.
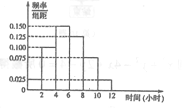
(1)应收集男生、女生样本数据各多少人?
(2)估计我校高二年级学生每周平均使用手机上网时间超过4小时的概率.
(3)将平均每周使用手机上网时间在![]() 内定义为“长时间使用手机”,在
内定义为“长时间使用手机”,在![]() 内定义为“短时间使用手机”.在样本数据中,有25名学生不近视.请完成下列2×2列联表,并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
内定义为“短时间使用手机”.在样本数据中,有25名学生不近视.请完成下列2×2列联表,并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
近视 | 不近视 | 合计 | |
长时间使用手机上网 | |||
短时间使用手机上网 | 15 | ||
合计 | 25 |
附:![]()
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 6.635 | 7.879 |