Question

【题目】已知椭圆的焦距为，且经过点．

（1）求椭圆的方程；

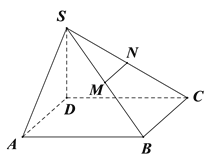
（2）A是椭圆与y轴正半轴的交点，椭圆上是否存在两点M，N，使得△AMN是以A为直角顶点的等腰直角三角形？若存在，请说明有几个，并求出直线MN；若不存在，请说明理由．

Answer 1

【答案】（Ⅰ）；（Ⅱ）存在，有3个．

【解析】

试题先用待定系数法求出椭圆方程，因为，直角边AM，AN不可能垂直或平行于轴，设的斜率为，则的斜率为，写出的直线方程，分别与椭圆方程联立，解出点的坐标，同理把，写出点的坐标，求出，由，列出方程求出值.

试题解析：(Ⅰ)由题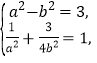解得，．所以椭圆Ω的方程为．

(Ⅱ)由题意可知，直角边AM，AN不可能垂直或平行于轴，故可设AM所在直线的方程为，不妨设，则直线AM所在的方程为．

联立方程消去整理得，解得，将代入可得，故点 .

所以．

同理可得，由，得，

所以，则，解得或．

当AM斜率时，AN斜率；当AM斜率时，AN斜率；当AM斜率时，AN斜率．

综上所述，符合条件的三角形有个.