题目内容
8.已知定义在R上的函数f(x)满足①f(2-x)=f(x);②f(x+2)=f(x-2);③x1,x2∈[1,3]时,$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0,则f(2014),f(2015),f(2016)大小关系为( )| A. | f(2014)>f(2015)>f(2016) | B. | f(2016)>f(2014)>f(2015) | ||
| C. | f(2016)=f(2014)>f(2015) | D. | f(2014)>f(2015)=f(2016) |
分析 根据已知可得函数 f (x)的图象关于直线x=1对称,周期为4,且在[1,3]上为减函数,进而可比较f(2014),f(2015),f(2016)的大小
解答 解:∵函数 f (x)满足:
①f(2-x)=f(x),故函数的图象关于直线x=1对称;
②f(x+2)=f(x-2),故函数的周期为4;
③x1,x2∈[1,3]时,$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0,故函数在[1,3]上为减函数;
故f(2014)=f(2),
f(2015)=f(3),
f(2016)=f(0)=f(2),
故f (2016)=f (2014)>f (2015),
故选:C.
点评 本题考查的知识点是函数的对称性,函数的周期性,函数的单调性,从已知的条件中分析出函数的性质,是解答的关键.

练习册系列答案
相关题目
13.函数f(x)=2x3+5$\sqrt{2{x^3}-1}$的最小值是( )
| A. | -3? | B. | 1 | C. | $-\frac{21}{4}$? | D. | 7 |
 已知四棱锥ABCD-A1B1C1D1的底面是边长为2的正方形,侧棱AA1⊥底面ABCD,若得二面角A1-BD-C1的大小为60°,求四棱柱ABCD-A1B1C1D1的体积.
已知四棱锥ABCD-A1B1C1D1的底面是边长为2的正方形,侧棱AA1⊥底面ABCD,若得二面角A1-BD-C1的大小为60°,求四棱柱ABCD-A1B1C1D1的体积.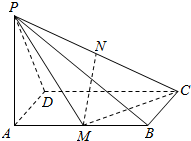 如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,AB=$\sqrt{2}$a.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,AB=$\sqrt{2}$a.