题目内容
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣
(t为参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣ ![]() .
.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C2上的动点,求PQ中点M到直线C3:
,Q为C2上的动点,求PQ中点M到直线C3: ![]() (α为参数)距离的最小值.
(α为参数)距离的最小值.
【答案】
(1)解:∵曲线C1的参数方程为 ![]() (t为参数),
(t为参数),
∴ ![]() ,
,
∴曲线C1的普通方程为(x+4)2+(y﹣3)2=1.
∵曲线C2的极坐标方程为ρ=﹣ ![]() ,
,
∴ρ2+8ρ2sin2θ=36,∴x2+y2+8y2=36,
∴曲线C2的直角坐标方程为 ![]() =1
=1
(2)解:∵C1上的点P对应的参数为t= ![]() ,∴P(﹣4,4),
,∴P(﹣4,4),
∵Q为C2上的动点,∴Q(6cosθ,2sinθ),
∴PQ中点M(﹣2+3cosθ,2+sinθ),
∵直线C3: ![]() (α为参数),
(α为参数),
∴C3为直线x+ ![]() y+6
y+6 ![]() =0,
=0,
∴点M到C1的距离:
d= ![]() =|4
=|4 ![]() |,
|,
∴当sin( ![]() )=﹣1时,PQ中点M到直线C3:
)=﹣1时,PQ中点M到直线C3: ![]() (α为参数)距离的最小值:
(α为参数)距离的最小值:
dmin=3 ![]() ﹣1
﹣1
【解析】(1)曲线C1的参数方程中利用sin2t+cos2t=1,消去参数t,能求出曲线C1的普通方程;曲线C2的极坐标方程中利用ρ2=x2+y2 , y=ρsinθ,能求出曲线C2的直角坐标方程.(2)先求出P(﹣4,4),Q(6cosθ,2sinθ),从而求出PQ中点M的坐标,再求出直线C3的直角坐标方程,由此利用点到直线的距离公式能求出PQ中点M到直线C3的距离的最小值.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出![]() 次成功交易,并对其评价进行统计爱,商品和服务评价的
次成功交易,并对其评价进行统计爱,商品和服务评价的![]() 列联表如下表:
列联表如下表:
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 |
|
|
|
对商品不满意 |
|
|
|
合计 |
|
|
|
(1)是否可以在犯错误概率不超过![]() 的前提下,认为商品好评与服务好评有关?
的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的![]() 次购物中,设对商品和服务全好评的次数为随机变量
次购物中,设对商品和服务全好评的次数为随机变量![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(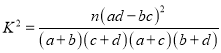 ,其中
,其中![]() )
)
【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟) |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为![]() 分钟.
分钟.
(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设![]() 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).

