题目内容
【题目】甲、乙两袋装有大小相同的红球和白球，甲袋装有2个红球和2个白球，乙袋装有2个红球和n个白球．现从甲、乙两袋中各任取2个球．
（1）若
，求取到的4个球全是红球的概率；
（2）若取到的4个球中至少有2个红球的概率为
，求n．
【答案】（1）
（2）
【解析】
(1)记“取到的4个球全是红球”为事件A，分别计算从甲乙两袋中取出的都是红球的概率，由相互独立事件的概率乘法公式计算可得答案.
(2)记“取到的4个球至多有一个红球”为事件B，“取到的4个球只有1个红球”为事件
，“取到的4个球全是白球”为事件
，将三个事件的概率表示出来，由
可得关于
的关系式，计算可得答案.
（1）解：记“取到的4个球全是红球”为事件A，取到的4个球全是红球的概率为
；
（2）解：记“取到的4个球至多有一个红球”为事件B，“取到的4个球只有1个红球”为事件，“取到的4个球全是白球”为事件，
由已知得
，即
，
亦即
，
，解得
（舍去），
练习册系列答案
相关题目
【题目】某中学某社团为研究高三学生课下钻研数学时间与数学考试中的解答题得分的关系，随机调查了某中学高三某班
名学生每周课下钻研数学时间
(单位：小时)与高三下学期期中考试数学解答题得分
，数据如下表：
| 2 | 4 | 6 | 8 | 10 | 12 |
| 30 | 38 | 44 | 48 | 50 | 54 |
（1）根据上述数据，求出数学考试中的解答题得分与该学生课下钻研数学时间的线性回归方程，并预测某学生每周课下钻研数学时间为
小时其数学考试中的解答题得分；
（2）从这人中任选
人，求人中至少有
人课下钻研数学时间不低于
小时的概率.
参考公式：
，其中
，
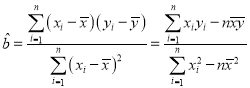；参考数据：
