题目内容
4．
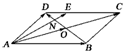如图，在平行四边形ABCD中，O是对角线AC，BD的交点，N是线段OD的中点，AN的延长线与CD交于点E，若$\overrightarrow{AE}$=m$\overrightarrow{AB}$+$\overrightarrow{AD}$，求实数m的值．
分析 由平行四边形的性质可得：△ABN～△DNE，再利用向量的三角形法则即可得出．
解答 解：由平行四边形ABCD可得：△ABN～△DNE，
则$\frac{DE}{AB}=\frac{DN}{BN}=\frac{1}{3}$，
即$\overrightarrow{AE}$=$\overrightarrow{DE}$+$\overrightarrow{AD}$=$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$，
∵$\overrightarrow{AE}$=m$\overrightarrow{AB}$+$\overrightarrow{AD}$，
∴m=$\frac{1}{3}$．
点评 本题考查了平行四边形的性质、向量的三角形法则，根据三角形的相似关系是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知点C在圆O直径BE的延长线上，CA切圆O于点A，CD是∠ACB的平分线，交AE于点F，交AB于点D．
一个小商店从某食品有限公司购进10袋白糖，称池内各袋白糖的重量（单位：g），如茎叶图所示，其中有一个数据被污损．
16．偶函数f（x）满足f（x）=f（2-x），且当x∈[-1，0]时，f（x）=cos$\frac{πx}{2}$-1，若函数g（x）=f（x）-logax有且仅有三个零点，则实数a的取值范围是（ ）
| A． | $（{\frac{1}{5}，\frac{1}{3}}）$ | B． | $（{\frac{1}{4}，\frac{1}{2}}）$ | C． | （2，4） | D． | （3，5） |