题目内容
12．求导函数：f（x）=$\frac{{x}^{3}-2}{2（x-1）^{2}}$．分析 根据函数的导数公式进行求导即可．
解答 解：函数的导数f′（x）=$\frac{3{x}^{2}×2（x-1）^{2}-（{x}^{3}-2）[4（x-1）]}{[2（x-1）^{2}]^{2}}$=$\frac{6{x}^{2}（x-1）^{2}-4（{x}^{3}-2）（x-1）}{[2（x-1）^{2}]^{2}}$
=$\frac{6{x}^{2}（x-1）-4（{x}^{3}-2）}{4（x-1）^{3}}$=$\frac{{x}^{3}-3{x}^{2}+4}{2（x-1）^{3}}$．
点评 本题主要考查函数的导数的计算，根据导数的运算法则是解决本题的关键．
练习册系列答案
相关题目
已知F1、F2是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点，以BF2为直径的圆D经过椭圆的上顶点A，且|$\overrightarrow{B{F}_{2}}$|=2|$\overrightarrow{A{F}_{1}}$|，$\overrightarrow{{F}_{1}A}•\overrightarrow{BA}$=24．
7．在△ABC中，若sin2B＞sin2A+sin2C，则△ABC是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 不能确定 |
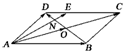如图，在平行四边形ABCD中，O是对角线AC，BD的交点，N是线段OD的中点，AN的延长线与CD交于点E，若$\overrightarrow{AE}$=m$\overrightarrow{AB}$+$\overrightarrow{AD}$，求实数m的值．