题目内容
17.给出下列四个命题:①已知函数f(x)=$\left\{\begin{array}{l}{1,(x为有理数)}\\{0,(x为无理数)}\end{array}\right.$,则f(x)为偶函数;
②函数y=(x+1)2+1(x≥0)与函数y=-1+$\sqrt{x-1}$(x≥1)互为反函数;
③函数f(x)=e-xx2在x=2处取得极大值;
④已知函数y=f(x)的图象在M(1,f(1))处的切线方程是y=$\frac{1}{2}$x+2,则f(1)+f′(1)=3.
其中真命题的代号是①②③④(写出所有真命题的代号).
分析 ①.利用函数的奇偶性的定义即可判断出正误;
②.利用反函数的求法即可判断出正误;
③.利用导数研究函数的单调性极值,即可判断出正误;
④.由已知可得:f(1)=$\frac{1}{2}+2$,f′(1)=$\frac{1}{2}$,即可判断出正误.
解答 解:①已知函数f(x)=$\left\{\begin{array}{l}{1,(x为有理数)}\\{0,(x为无理数)}\end{array}\right.$,设x为有理数,则-x也为有理数,∴f(-x)=1=f(x),同理当x为无理数时,也有f(-x)=f(x)=0,因此f(x)为偶函数,因此正确;
②由函数y=(x+1)2+1(x≥0),解出x=-1+$\sqrt{y-1}$,把x与y互换可得:y=-1+$\sqrt{x-1}$(x≥1),因此函数y=(x+1)2+1(x≥0)与函数y=-1+$\sqrt{x-1}$(x≥1)互为反函数,正确;
③函数f(x)=e-xx2,f′(x)=-e-xx2+2xe-x=xe-x(2-x),当x>2时,f′(x)<0,此时函数f(x)单调递减;当x<2时,f′(x)>0,此时函数f(x)单调递增,因此x=2处取得极大值,正确;
④已知函数y=f(x)的图象在M(1,f(1))处的切线方程是y=$\frac{1}{2}$x+2,则f(1)=$\frac{1}{2}+2$,f′(1)=$\frac{1}{2}$,∴f(1)+f′(1)=3,因此正确.
其中真命题的代号是 ①②③④.
故答案为:①②③④.
点评 本题考查了函数的奇偶性的定义、反函数的求法、利用导数研究函数的单调性极值切线方程及其几何意义、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.如图所示的数阵中,每行、每列的三个数均成等比数列,如果数阵中所有数的乘积等于$\frac{1}{512}$,那么a22=( )
$(\begin{array}{l}{{a}_{11}}&{{a}_{12}}&{{a}_{13}}\\{{a}_{21}}&{{a}_{22}}&{{a}_{23}}\\{{a}_{31}}&{{a}_{32}}&{{a}_{33}}\end{array})$.
$(\begin{array}{l}{{a}_{11}}&{{a}_{12}}&{{a}_{13}}\\{{a}_{21}}&{{a}_{22}}&{{a}_{23}}\\{{a}_{31}}&{{a}_{32}}&{{a}_{33}}\end{array})$.
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
2.已知命题p:?x0∈R,x02+x0+1≤0,则¬p为( )
| A. | ?x0∈R,x02+x0+1>0 | B. | ?x0∉R,x02+x0+1>0 | ||
| C. | ?x∈R,x2+x+1>0 | D. | ?x∈R,x2+x+1≥0 |
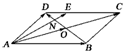 如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,若$\overrightarrow{AE}$=m$\overrightarrow{AB}$+$\overrightarrow{AD}$,求实数m的值.
如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,若$\overrightarrow{AE}$=m$\overrightarrow{AB}$+$\overrightarrow{AD}$,求实数m的值.
 如图所示,AB为⊙O的直径,O为圆心,PB与⊙O相切于点B,PO交⊙O于点D,AD的延长线交PB于点C,若AB=2,PB=2$\sqrt{2}$,则BC=$\sqrt{2}$.
如图所示,AB为⊙O的直径,O为圆心,PB与⊙O相切于点B,PO交⊙O于点D,AD的延长线交PB于点C,若AB=2,PB=2$\sqrt{2}$,则BC=$\sqrt{2}$.