题目内容
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a. 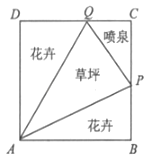
(1)当∠PAQ= ![]() 时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
(2)考虑到小区道路的整体规划,要求PB+DQ=PQ,请探究∠PAQ是否为定值,若是,求出此定值,若不是,请说明理由.
【答案】
(1)解:∵边长为1百米的正方形ABCD中,∠PAB=a,∠PAQ= ![]() ,
,
∴PB=100tanα,DQ=100tan( ![]() ﹣α﹣
﹣α﹣ ![]() )=100tan(
)=100tan( ![]() ﹣α),
﹣α),
∴S花卉种植面积=S△ABP+S△ADQ= ![]() =
= ![]() 100×100tanα+
100×100tanα+ ![]() 100tan(
100tan( ![]() ﹣α)
﹣α)
= ![]() =
= 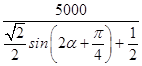 ,其中α∈[0,
,其中α∈[0, ![]() ],
],
∴当sin(2α+ ![]() )=1时,即θ=
)=1时,即θ= ![]() 时,S取得最小值为5000(2﹣
时,S取得最小值为5000(2﹣ ![]() ).
).
(2)解:设∠PAB=α,∠QAD=β,CP=x,CQ=y,则BP=100﹣x,DQ=100﹣y,
在△ABP中,tanα= ![]() ,在△ADQ中,tanβ=
,在△ADQ中,tanβ= ![]() ,
,
∴tan(α+β)= ![]() =
= 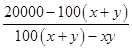 ,
,
∵PB+DQ=PQ,
∴100﹣x+100﹣y= ![]() ,整理可得:x+y=100+
,整理可得:x+y=100+ ![]() ,
,
∴tan(α+β)= 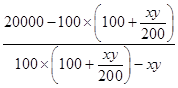 =
= 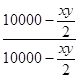 =1,
=1,
∴α+β= ![]() ,
,
∴∠PAQ是定值,且∠PAQ= ![]() .
.
【解析】(1)由已知利用三角函数的定义可求PB=100tanα,DQ=100tan( ![]() ﹣α),利用三角形面积公式及三角函数恒等变换的应用化简可求S花卉种植面积=
﹣α),利用三角形面积公式及三角函数恒等变换的应用化简可求S花卉种植面积= ![]() ,其中α∈[0,
,其中α∈[0, ![]() ],利用正弦函数的性质可求最小值.(2)设∠PAB=α,∠QAD=β,CP=x,CQ=y,则可求BP,DQ,利用两角和的正切函数公式可求tan(α+β)=
],利用正弦函数的性质可求最小值.(2)设∠PAB=α,∠QAD=β,CP=x,CQ=y,则可求BP,DQ,利用两角和的正切函数公式可求tan(α+β)= ![]() ,由题意PB+DQ=PQ,可求:x+y=100+
,由题意PB+DQ=PQ,可求:x+y=100+ ![]() ,即可得解tan(α+β)=1,可求α+β=
,即可得解tan(α+β)=1,可求α+β= ![]() ,即可得解.
,即可得解.
【考点精析】掌握正弦定理的定义是解答本题的根本,需要知道正弦定理:![]() .
.

 口算能手系列答案
口算能手系列答案