题目内容
【题目】若函数f（x）对于定义域内的任意x都满足 
，则称f（x）具有性质M．
（1）很明显，函数 
（x∈（0，+∞）具有性质M；请证明 （x∈（0，+∞）在（0，1）上是减函数，在（1，+∞）上是增函数．
（2）已知函数g（x）=|lnx|，点A（1，0），直线y=t（t＞0）与g（x）的图象相交于B、C两点（B在左边），验证函数g（x）具有性质M并证明|AB|＜|AC|．
（3）已知函数 
，是否存在正数m，n，k，当h（x）的定义域为[m，n]时，其值域为[km，kn]，若存在，求k的范围，若不存在，请说明理由．
【答案】
（1）解：∵f（ 
）= + 
=x+ =f（x），∴函数f（x）具有性质M．
任取x1、x2且x1＜x2，
则f（x1）﹣f（x2）=（x1+ 
）﹣（x2+ 
）=（x1﹣x2）+（ ﹣ ）=（x1﹣x2） 
，
若x1、x2∈（0，1），
则0＜x1x2＜1，x1x2＞0，x1﹣x2＜0，
∴f（x1）﹣f（x2）＞0，
∴f（x1）＞f（x2），
∴f（x）在（0，1）上是减函数．
若x1、x2∈（1，+∞），
则x1x2＞1，x1﹣x2＜0，
∴f（x1）﹣f（x2）＜0，
∴f（x1）＜f（x2），
∴f（x）在（1，+∞）上是增函数．
（2）解：∵ 
，∴g（x）具有性质M
由|lnx|=t得，lnx=﹣t或lnx=t，x=e﹣t或x=et，
∵t＞0，∴e﹣t＜et，
∴ 
，
∴ 
，∴ 
，
∴|AB|2﹣|AC|2=（1﹣e﹣t）2﹣（1﹣et）2=[2﹣（e﹣t+et）]（et﹣e﹣t）
由（1）知， 
在x∈（0，+∞）上的最小值为1（其中x=1时）
而 
，故2﹣（e﹣t+et）＜0，et﹣e﹣t＞0，
|AB|＜|AC|
（3）解：∵h（1）=0，m，n，k均为正数，
∴0＜m＜n＜1或1＜m＜n
当0＜m＜n＜1时，0＜x＜1， 
= 
是减函数，
值域为（h（n），h（m）），h（n）=km，h（m）=kn，
∴ 
，∴ 
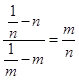，∴1﹣n2=1﹣m2
故不存在
当1＜m＜n时，x＞1， = 
是增函数，
∴h（m）=km，h（n）=kn，∴ 
，
∴（1﹣k）m2=1，（1﹣k）n2=1， 
，不存在
综合得，若不存在正数m，n，k满足条件
【解析】（1）根据函数单调性的定义进行证明即可，（2）根据函数的性质利用作差法进行判断即可，（3）根据 函数定义域和值域的关系建立方程，进行求解即可．
