题目内容
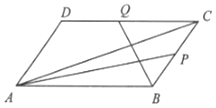
【题目】如图，在平行四边形ABCD中，P，Q分别是BC和CD的中点． 
（1）若AB=2，AD=1，∠BAD=60°，求 
及cos∠BAC的余弦值；
（2）若 =λ 
+ 
，求λ+μ的值．
【答案】
（1）解：∵平行四边形ABCD中，AB=2，AD=1，∠BAD=60°，
∴ 
= （ + 
）= 2+ =22+2×1×cos60°=5，
| |2= 2=（ + ）2= 2+2 + 2=22+2×2×1×cos60°+1=7，
∴| |= 
，
cos∠BAC=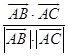 
= 
= 
；
（2）解：∵P，Q分别是BC和CD的中点．
∴ 
= + 
， 
= ﹣ 
，
∵ =λ + 
，
∴ + =λ（ + ）+μ（ ﹣ ），
∴ 
，
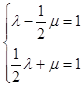解得：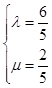 
，
∴λ+μ= 
【解析】（1）由已知中AB=2，AD=1，∠BAD=60°，代入向量数量积公式，可得 
，求出| |，代入cos∠BAC=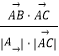 
可得cos∠BAC的余弦值；（2）若 =λ 
+ 
，则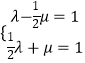 
，解得答案．
练习册系列答案
相关题目
