题目内容
椭圆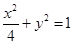 的焦点为
的焦点为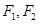 ,点
,点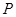 在椭圆上,且线段
在椭圆上,且线段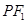 的中点恰好在
的中点恰好在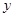 轴上,
轴上,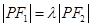 ,则
,则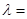 .
.
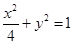 的焦点为
的焦点为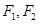 ,点
,点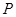 在椭圆上,且线段
在椭圆上,且线段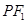 的中点恰好在
的中点恰好在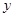 轴上,
轴上,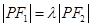 ,则
,则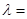 .
.
试题分析:易知,原点也是
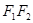 的中点,所以
的中点,所以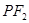 平行于
平行于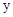 轴,因为
轴,因为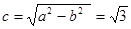 ,所以
,所以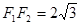 ,
,设
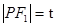 ,根据椭圆定义可知
,根据椭圆定义可知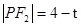 ,所以
,所以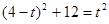 ,解得
,解得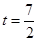 ,所以
,所以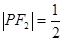 ,故
,故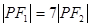 ,所以
,所以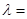 7.
7.点评:本题重点考查椭圆的几何性质,考查椭圆定义的应用,属于基础题.

练习册系列答案
相关题目
题目内容
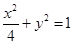 的焦点为
的焦点为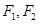 ,点
,点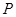 在椭圆上,且线段
在椭圆上,且线段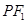 的中点恰好在
的中点恰好在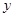 轴上,
轴上,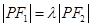 ,则
,则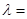 .
.
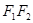 的中点,所以
的中点,所以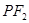 平行于
平行于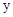 轴,因为
轴,因为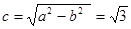 ,所以
,所以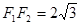 ,
,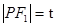 ,根据椭圆定义可知
,根据椭圆定义可知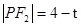 ,所以
,所以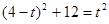 ,解得
,解得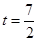 ,所以
,所以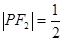 ,故
,故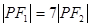 ,所以
,所以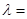 7.
7.