题目内容
过椭圆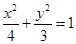 的右焦点
的右焦点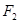 的直线交椭圆于于
的直线交椭圆于于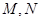 两点,令
两点,令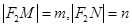 ,则
,则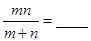 。
。
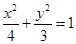 的右焦点
的右焦点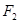 的直线交椭圆于于
的直线交椭圆于于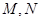 两点,令
两点,令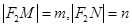 ,则
,则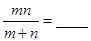 。
。
试题分析:不舍一般性,不妨取MN垂直x轴的情况,此时MN:x=1,联立
 ,得M(1,
,得M(1, ),N(1,-
),N(1,- ),∴m=n=
),∴m=n= ,∴
,∴
点评:解决本题的关键是挖出图形中的隐含关系,得出基本量之间的关系,属基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
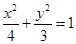 的右焦点
的右焦点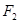 的直线交椭圆于于
的直线交椭圆于于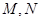 两点,令
两点,令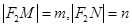 ,则
,则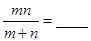 。
。
 ,得M(1,
,得M(1, ),N(1,-
),N(1,- ),∴m=n=
),∴m=n= ,∴
,∴

 阅读快车系列答案
阅读快车系列答案