题目内容
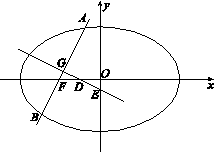
如图,已知椭圆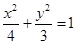 的左焦点为
的左焦点为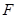 ,过点
,过点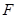 的直线交椭圆于
的直线交椭圆于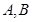 两点,线段
两点,线段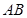 的中点为
的中点为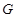 ,
,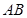 的中垂线与
的中垂线与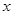 轴和
轴和 轴分别交于
轴分别交于 两点.
两点.
(1)若点 的横坐标为
的横坐标为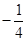 ,求直线
,求直线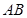 的斜率;
的斜率;
(2)记△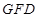 的面积为
的面积为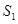 ,△
,△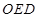 (
(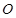 为原点)的面积为
为原点)的面积为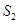 .试问:是否存在直线
.试问:是否存在直线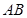 ,使得
,使得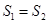 ?说明理由.
?说明理由.
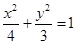 的左焦点为
的左焦点为 ,过点
,过点 的直线交椭圆于
的直线交椭圆于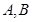 两点,线段
两点,线段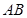 的中点为
的中点为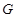 ,
,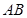 的中垂线与
的中垂线与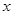 轴和
轴和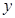 轴分别交于
轴分别交于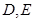 两点.
两点.
(1)若点
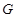 的横坐标为
的横坐标为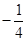 ,求直线
,求直线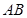 的斜率;
的斜率;(2)记△
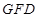 的面积为
的面积为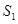 ,△
,△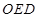 (
(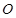 为原点)的面积为
为原点)的面积为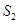 .试问:是否存在直线
.试问:是否存在直线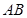 ,使得
,使得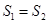 ?说明理由.
?说明理由.(1)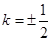 (2)不存在直线
(2)不存在直线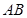 ,使得
,使得 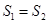
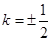 (2)不存在直线
(2)不存在直线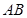 ,使得
,使得 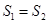
试题分析:(Ⅰ)解:依题意,直线
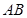 的斜率存在,设其方程为
的斜率存在,设其方程为 .
. 将其代入
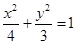 ,整理得
,整理得  .
. 设
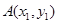 ,
, ,所以
,所以  . 3分
. 3分故点
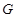 的横坐标为
的横坐标为 .依题意,得
.依题意,得 ,
,解得
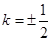 . 5分
. 5分(Ⅱ)解:假设存在直线
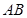 ,使得
,使得 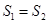 ,显然直线
,显然直线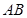 不能与
不能与 轴垂直.
轴垂直.
由(Ⅰ)可得
 . 6分
. 6分因为
 ,所以
,所以  ,
, 解得
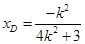 , 即
, 即  . 8分
. 8分因为 △
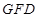 ∽△
∽△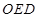 ,所以
,所以  .
. 所以
 , 10分
, 10分整理得
 .
.因为此方程无解,所以不存在直线
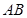 ,使得
,使得 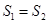 . 12分
. 12分点评:直线与椭圆相交时常联立方程借助于方程根与系数的关系整理化简,此类题目计算量较大要求学生具有较高的数据处理能力

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
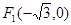 和
和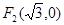 ,且椭圆过点
,且椭圆过点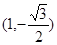 .
.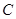 的方程;
的方程;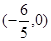 作不与
作不与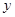 轴垂直的直线
轴垂直的直线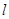 交该椭圆于
交该椭圆于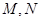 两点,
两点,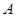 为椭圆的左顶点,试判断
为椭圆的左顶点,试判断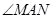 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.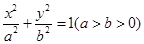 的左、右焦点分别为F1、F2,P是椭圆上的一点,
的左、右焦点分别为F1、F2,P是椭圆上的一点,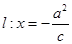 ,且
,且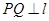 ,垂足为
,垂足为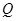 ,若四边形
,若四边形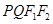 为平行四边形,则椭圆的离心率的取值范围是( )
为平行四边形,则椭圆的离心率的取值范围是( )



 :
: 的右焦点
的右焦点 在圆
在圆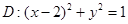 上,直线
上,直线 交椭圆于
交椭圆于 、
、 两点.
两点. (
( 为坐标原点),求
为坐标原点),求 的值;
的值;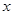 轴的对称点为
轴的对称点为 (
( ,试问
,试问 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.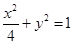 的焦点为
的焦点为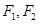 ,点
,点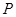 在椭圆上,且线段
在椭圆上,且线段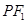 的中点恰好在
的中点恰好在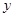 轴上,
轴上,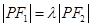 ,则
,则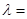 .
.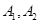 为椭圆
为椭圆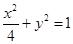 的左右顶点,在长轴
的左右顶点,在长轴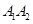 上随机任取点
上随机任取点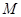 ,过
,过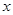 轴的直线交椭圆于点
轴的直线交椭圆于点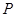 ,则使
,则使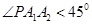 的概率为
的概率为



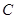 的中心在原点,焦点在
的中心在原点,焦点在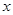 轴上,离心率为
轴上,离心率为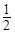 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线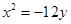 的焦点.
的焦点.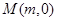 的直线
的直线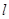 与椭圆
与椭圆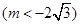 ,直线
,直线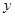 轴交于点
轴交于点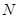 ,当
,当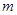 为何值时
为何值时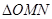 的面积有最小值?并求出最小值.
的面积有最小值?并求出最小值.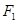 、
、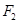 是椭圆
是椭圆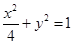 的左、右焦点,弦
的左、右焦点,弦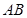 过
过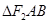 的周长为 .
的周长为 .