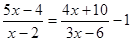题目内容
已知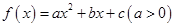 ,当
,当 时,
时, .
.
(1)证明: ;
;
(2)若 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 值的特点求出函数
值的特点求出函数 的表达式.
的表达式.
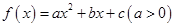 ,当
,当 时,
时, .
.(1)证明:
 ;
;(2)若
 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 值的特点求出函数
值的特点求出函数 的表达式.
的表达式.(1)详见解析;(2)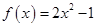 .
.
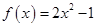 .
.试题分析:(1)根据题中条件并利用
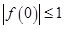 得到
得到 ;(2)先利用题中条件得到
;(2)先利用题中条件得到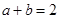 ,并结合
,并结合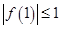 得到
得到 的取值范围,结合(1)中的结论求出
的取值范围,结合(1)中的结论求出 值,然后借助题中条件分析出函数是
值,然后借助题中条件分析出函数是 的图象关于
的图象关于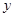 轴对称,从而求出
轴对称,从而求出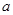 与
与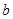 的值,从而最终确定函数
的值,从而最终确定函数 的解析式.
的解析式.试题解析:(1)
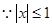 时
时 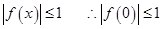
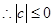 4分
4分(2)由
 得到
得到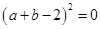
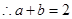 5分
5分又
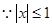 时
时 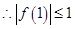 即
即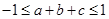
将
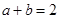 代入上式得
代入上式得 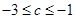 又
又 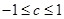
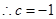 8分
8分又
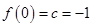
 时
时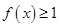
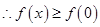
对
 均成立
均成立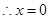 为函数
为函数 为对称轴 10分
为对称轴 10分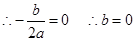 又
又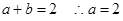
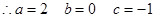 12分
12分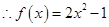 13分
13分
练习册系列答案
相关题目
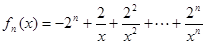 .
.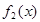 在
在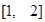 上的值域;
上的值域;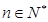 ,在
,在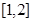 上存在唯一的
上存在唯一的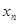 ,使得
,使得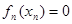 ;
;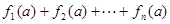 的值.
的值. ,若
,若 且对任意实数
且对任意实数 均有
均有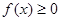 成立.
成立. 表达式;
表达式; 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围.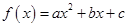 .
.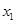 、
、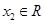 ,且
,且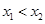 ,都有
,都有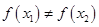 ,求证:关于
,求证:关于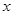 的方程
的方程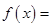
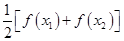 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于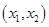 ;
;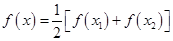 在
在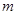 ,且
,且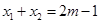 ,设函数
,设函数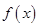 的图象的对称轴方程为
的图象的对称轴方程为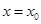 ,求证:
,求证: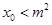 .
. 的图像与函数h(x)=x++2的图像关于点A(0,1)对称.
的图像与函数h(x)=x++2的图像关于点A(0,1)对称. ,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.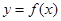 在区间
在区间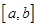 上存在
上存在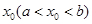 ,满足
,满足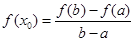 ,则称
,则称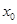 是函数
是函数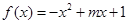 在区间
在区间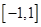 上存在均值点,则实数
上存在均值点,则实数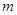 的取值范围是 .
的取值范围是 .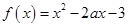 在区间
在区间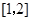 上是单调函数的条件是( )
上是单调函数的条件是( )