题目内容
已知二次函数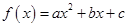 .
.
(1)若对任意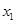 、
、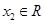 ,且
,且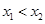 ,都有
,都有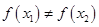 ,求证:关于
,求证:关于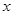 的方程
的方程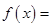
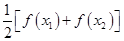 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于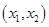 ;
;
(2)若关于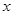 的方程
的方程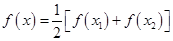 在
在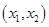 上的根为
上的根为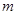 ,且
,且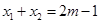 ,设函数
,设函数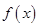 的图象的对称轴方程为
的图象的对称轴方程为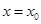 ,求证:
,求证: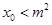 .
.
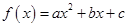 .
.(1)若对任意
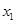 、
、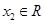 ,且
,且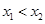 ,都有
,都有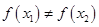 ,求证:关于
,求证:关于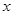 的方程
的方程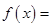
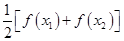 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于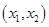 ;
;(2)若关于
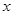 的方程
的方程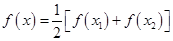 在
在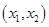 上的根为
上的根为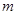 ,且
,且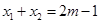 ,设函数
,设函数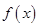 的图象的对称轴方程为
的图象的对称轴方程为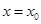 ,求证:
,求证: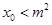 .
.(1)详见解析;(2)详见解析.
试题分析:(1)先构造新函数
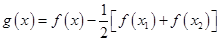 ,利用
,利用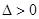 证明方程
证明方程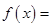
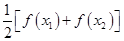 有两个不相等的实数根,然后利用存在定理证明方程
有两个不相等的实数根,然后利用存在定理证明方程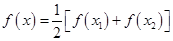 必有一个根属于
必有一个根属于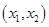 ,即利用
,即利用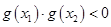 来证明;(2)将
来证明;(2)将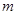 的代入方程
的代入方程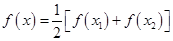 得到
得到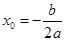 的表达式,结合
的表达式,结合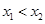 证明
证明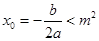 .
.试题解析:(1)构造函数
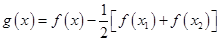
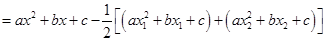
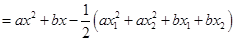 ,
,由于函数
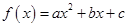 为二次函数,所以
为二次函数,所以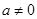 ,
,对于二次函数
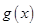 而言,
而言,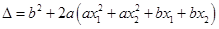
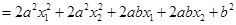

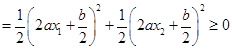 ,
,若
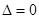 ,则有
,则有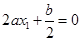 且有
且有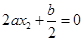 ,从而有
,从而有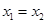 ,这与
,这与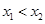 矛盾,
矛盾,故
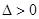 ,故方程
,故方程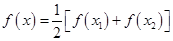 有两个不相等,
有两个不相等,由于
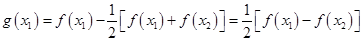 ,
,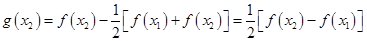 ,
,所以
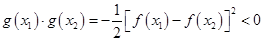 ,
,由零点存在定理知,方程
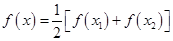 必有一个根属于
必有一个根属于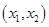 ;
;(2)由题意知
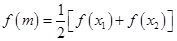 ,化简得
,化简得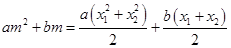 ,
,即
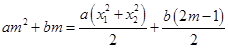 ,则有
,则有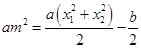 ,
,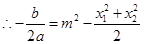 ,
,由于
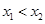 ,则
,则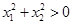 ,故
,故 ,即
,即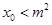 .
.
练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
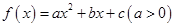 ,当
,当 时,
时, .
. ;
; 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 的表达式.
的表达式.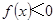 的解集为
的解集为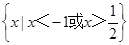 ,则
,则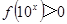 的解集为( )
的解集为( )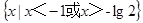
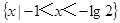
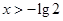 }
}  }
} 对
对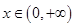 的图象恒在x轴上方,则m的取值范围是( )
的图象恒在x轴上方,则m的取值范围是( )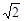 <m<2+2
<m<2+2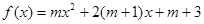 仅有一个负零点,则m的取值范围为( )
仅有一个负零点,则m的取值范围为( )



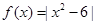 ,若
,若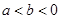 ,且
,且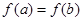 ,则
,则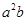 的最小值是 .
的最小值是 . ,若存在实数
,若存在实数 、
、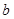 、
、 、
、 ,满足
,满足
 ,其中
,其中 ,则
,则 的取值范围是 .
的取值范围是 . 的解是
的解是 ,则m-n的值是
,则m-n的值是 的值域为
的值域为 ,则
,则 的取值范围是( )
的取值范围是( )


