��Ŀ����
����Ŀ��ij��Ϊ��Ӧ���ҽ��ܼ��Ž���ĺ��٣��������Ǵ��Լ����ߵ�С�����𣬿�չ���ԡ���С������Ҳ��һ��֧�֡�Ϊ�����������������������������棺 ��80���ֻ���һ��ͻ�����һ�ֶ����������ŷţ�
�������������������˵ı�����ʵ�ͬʱ��ȴ���ò����������ŷŵ�β����
���֯��Ϊ�˽���������������������Ч���������10��60�����Ⱥ�����n�ˣ��������������ѡȡ������������ʣ����������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������Ч�������������ʾ��
�����������
���һ | ���� | |||
�ش��� | ռ���� | �ش��� | ռ���� | |
[10��20�� | 90 | 0.5 | 45 | a |
[20��30�� | 225 | 0.75 | k | 0.8 |
[30��40�� | b | 0.9 | 252 | 0.6 |
[40��50�� | 160 | c | 120 | d |
[50��60] | 10 | e | f | g |
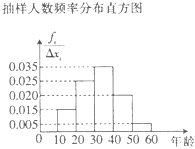
��1���ֱ�д��n��a��b��c��d��ֵ��
��2���������е�Ƶ�ʽ��ƿ�������������ȷ�ش������ݵĸ��ʣ��涨��ȷ�ش���һ�����ݵ�30Ԫ�����������ݵ�60Ԫ����֯�������һ��ͥ������Ա������45�꣬����17�꣩��ָ�����˻ش���һ�����ݣ����ӻش���������ݣ���ü�ͥ��ý������εķֲ��м�������
���𰸡�
��1���⣺������֪��[10��20�����г������Ϊ90��0.5=180�ˣ�
[10��20�����г��������Ƶ��Ϊ0.015��10=0.15��
��n=180��0.15=1200��
��a= ![]() =
= ![]() ��b=��252��0.6����0.9=378��
��b=��252��0.6����0.9=378��
c ![]() ��
��
d= ![]() =
= ![]()
��2���⣺������֪��������ȷ�ش���һ���ݵĸ���ΪP��A��= ![]() ��
��
������ȷ�ش���������ݵĸ���ΪP��B��= ![]() ��
��
��ο���ȡֵΪ0��30��60��90��
P����=0��=��1�� ![]() ����1��
����1�� ![]() ��=
��= ![]() ��
��
P����=30��= ![]() =
= ![]() ��
��
P����=60��=��1�� ![]() ��
�� ![]() =
= ![]() ��
��
P����=90��= ![]() =
= ![]() ��
��
��εķֲ���Ϊ��
�� | 0 | 30 | 60 | 90 |
P |
|
|
|
|
��E��= ![]() =35
=35
����������1������Ƶ�ʷֲ�ֱ��ͼ��ͳ�Ʊ���⣮��2��������֪��������ȷ�ش���һ���ݵĸ���ΪP��A��= ![]() ��������ȷ�ش���������ݵĸ���ΪP��B��=
��������ȷ�ش���������ݵĸ���ΪP��B��= ![]() ���ο���ȡֵΪ0��30��60��90���ֱ������Ӧ�ĸ��ʣ��ɴ�������ü�ͥ��ý������εķֲ��м�������
���ο���ȡֵΪ0��30��60��90���ֱ������Ӧ�ĸ��ʣ��ɴ�������ü�ͥ��ý������εķֲ��м�������
�����㾫����ͨ�����������ɢ�������������ֲ��У��������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��м����Խ����⣮

 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д�