Question

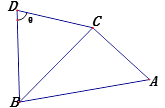
【题目】在如图四边形 中， 为的 内角 的对边，且满足 .

(Ⅰ)证明： 成等差数列；
(Ⅱ)已知 求四边形 的面积.

Answer 1

【答案】解：(Ⅰ)由题设有
即
由三角形内角和定理有 由正弦定理有
成等差数列.
(Ⅱ) 在 中，由余弦定理有 即
, 即 则 为 .
由于

【解析】(1)利用已知条件整理转化原有的代数式即可得到sin(A+B)+sin(A+C)=2sinA，根据三角形的内角和定理以及正弦定理即可求出 b + c = 2 a由等差数列的性质可得出b , a , c 成等差数列。(2)根据题意由余弦定理代入数值求出 B C = 4，再结合已知条件可分别求出 c = 5 、b = 3故可证明Δ A B C 为 R t Δ进而求出面积为6然后根据同角三角函数的基本关系式求出 sin ∠ C D B的值代入到三角形的面积公式求出结果。